课程 23 - 思维导图

有很多无限画布应用都提供了对于思维导图的支持，例如 miro、excalidraw、canva、xmind 等等。我非常喜欢 excalidraw 的分类方式，它把思维导图又细分成了三种子类型：

Spider mapping 适合头脑风暴场景，从最中心的核心主题伸展开去，形似一张蜘蛛网。从渲染效果上看，mermaid 提供的也是这种类型。
Tree mapping
Flow map

Spider mapping	Tree mapping	Flow map

这里我们仅讨论最后一种类型。

尽管思维导图最终的展现形式存在很大差异，但从数据结构上看，思维导图就是一棵树形结构，由节点和边组成。markmap、mermaid 通过将 markdown 转换成这种结构。树是一种特殊的图结构，也有一些针对有向图的布局算法例如 dagre 和 elkjs 等等，这里就不考虑了。

json

{
    "id": "Modeling Methods",
    "children": [
        {
            "id": "Classification",
            "children": []
        }
    ]
}

针对这类数据，d3-hierarchy 提供了一系列开箱即用的算法，同样我们仅关注 d3-tree 这一种。

d3-tree

我们先添加两个限制，后续会介绍如何突破它们：目标为二叉树，所有节点尺寸都相同（或者说不存在尺寸）。

d3-tree 的实现思路来自：Tidier Drawings of Trees，它在前人的研究基础上提出了几个美学标准：

Aesthetic 1: Nodes at the same level of the tree should lie along a straight line, and the straight lines defining the levels should be parallel.
Aesthetic 2: A left son should be positioned to the left of its father and a right son to the right.
Aesthetic 3: A father should be centered over its sons.
Aesthetic 4: A tree and its mirror image should produce drawings that are reflections of one another; moreover, a subtree should be drawn the same way regardless of where it occurs in the tree.

关于前三个标准的演变改进过程可以阅读 Drawing Presentable Trees，它使用 Python 代码和配图详细地展示了之前论文的算法思路。比如实现第三条标准很简单，就是使用后序遍历，将父节点的 x 坐标设置为所有子节点中最左和最右的中点：

// @see https://github.com/d3/d3-hierarchy/blob/main/src/tree.js#L150
var midpoint = (children[0].z + children[children.length - 1].z) / 2;

能很直观的看出来它仍然不够对称，整体偏右，这也引出了标准四：

As narrowly as possible	A parent should be centered over its children

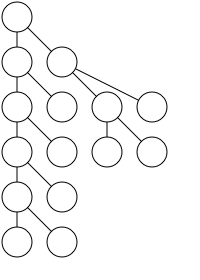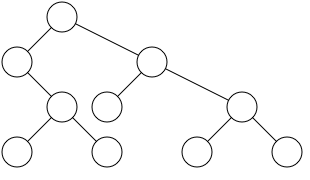居中父节点这一操作有可能与它的兄弟节点位置冲突，此时我们需要将子树整体移动，但如果用下面的递归方式，算法复杂度会来到 $O (n^{2})$ ：

python

def move_right(branch, n):
    branch.x += n
    for c in branch.children:
        move_right(c, n)

此时我们需要为节点增加一个 mod 属性，这样居中父节点操作可以暂时不考虑冲突，后续再进行移动。这样避免了递归，算法复杂度回到了 $O (n)$ 。另外也需要新增一个 prelim 属性，这个名称来自：A Node-Positioning Algorithm for General Trees：

// @see https://github.com/d3/d3-hierarchy/blob/main/src/tree.js#L67
function TreeNode(node, i) {
    this._ = node; // final position: _.x
    this.parent = null;
    this.children = null;
    this.z = 0; // prelim
    this.m = 0; // mod
}

正因为使用了后序遍历：

function tree(root) {
    var t = treeRoot(root);
    t.eachAfter(firstWalk);
    t.eachBefore(secondWalk);
}

在第二次前序遍历中递归累加 mod，完成向右平移得到最终的位置 _.x。这对应着原始论文中的 PETRIFY 步骤：

// @see https://github.com/d3/d3-hierarchy/blob/main/src/tree.js#L164
function secondWalk(v) {
    v._.x = v.z + v.parent.m; // final x
    v.m += v.parent.m;
}

这里需要引入 contour 的概念，例如下左树的右轮廓为 [1, 1, 2]，下右树的左轮廓为 [1, 0, 1]。当我们需要避免这两棵子树重合在一起，只需要比较这两个轮廓就能得出需要将右树向右移动多少距离，在这个例子中移动距离是 2。

python

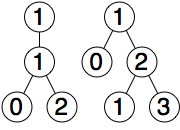
def push_right(left, right):
    wl = contour(left, lt)
    wr = contour(right, gt)
    return max(x-y for x,y in zip(wl, wr)) + 1

得到子树轮廓的算法依然需要递归，因此复杂度为 $O (n^{2})$ 。为了优化引入了 thread 的概念，下图中虚线就表示这种有别于父子的关系，将每棵子树原本可能并不实际存在的轮廓勾勒了出来：

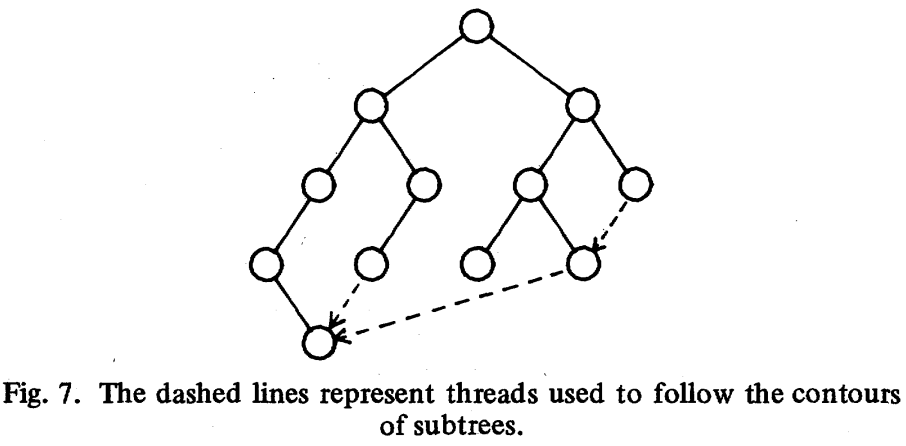
function TreeNode(node, i) {
    this.t = null; // thread
}

这样在计算 contour 时就可以跨越实际的层次结构，直接通过 thread 获取，这样复杂度也降为了 $O (n)$ ：

// @see https://github.com/d3/d3-hierarchy/blob/main/src/tree.js#L15C1-L24C2
function nextLeft(v) {
    var children = v.children;
    return children ? children[0] : v.t;
}
function nextRight(v) {
    var children = v.children;
    return children ? children[children.length - 1] : v.t;
}

复杂度证明

让我们来回顾一下该算法。首先进行一趟后序遍历计算节点的相对坐标和 thread，然后进行一趟前序遍历累加 mod，确定每个节点的绝对坐标位置。不难看出每个节点在这两趟遍历中都只会被访问一次。因此只需要确定第一趟遍历中轮廓扫描的复杂度。

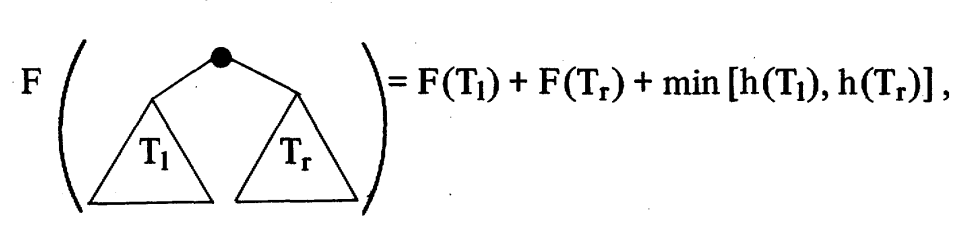
在原论文中对这一步的复杂度也进行了数学分析。 $F (T)$ 表示“在整个树 T 中，轮廓扫描总共需要访问多少个节点？”。其中子树的 $h (T)$ 表示从根节点到叶节点的最大深度，也就是路径节点数 - 1。它代表了轮廓扫描时最坏情况的访问深度，当一层层比较两个轮廓的间距时，一旦任意一方的轮廓到底了（没有更深的层），就停止扫描了，因此这里使用的是 $m i n ()$ ：

接下来只需要证明 $F (T) \leq n (T)$ 即可，其中 $n (T)$ 代表子树拥有的全部节点数量。这样就能确定整个算法复杂度为 $O (n)$ 。

作者提出了这样一个假设： $F (T) = n (T) - h (T)$ 。依据是每个内部节点（非叶子）最多会参与一次轮廓比较，而叶子节点不需要扫描，因为没有子树要比较，整棵树共有 $n (T)$ 个节点，其中至少有 $h (T)$ 个叶子在最深路径上，所以最多只有 $n (T) - h (T)$ 个节点需要参与轮廓扫描。因此这其实确定了扫描访问节点数的上界，接下来只需要证明对任意树 $T$ ，轮廓扫描访问的节点数 $S c a n (T) \leq F (T)$

使用归纳法， $N = 0$ （此时无需扫描）和 $N = 1$ 时成立。假设 $S c a n (T) \leq F (T) = n (T) - h (T)$ 。

根据定义（加上根节点）：

\begin{aligned} n (T) & = 1 + n (T_{l}) + n (T_{r}) \\ h (T) & = 1 + m a x (h (T_{r}), h (T_{r})) \end{aligned}

代入：

\begin{aligned} F (T) & = n (T) - h (T) \\ = 1 + n (T_{l}) + n (T_{r}) - [1 + m a x (h (T_{l}), h (T_{r}))] \\ = [n (T_{l}) - h_{l}] + [n (T_{r}) - h_{r}] + [h_{l} + h_{r} - m a x (h_{l}, h_{r})] \\ \geq F (T_{l}) + F (T_{r}) + m i n (h_{l}, h_{r}) \end{aligned}

因此： $F (T) \geq F (T_{l}) + F (T_{r}) + m i n (h (T_{l}), h (T_{r})) \geq S c a n (T)$

扩展到 N 叉树

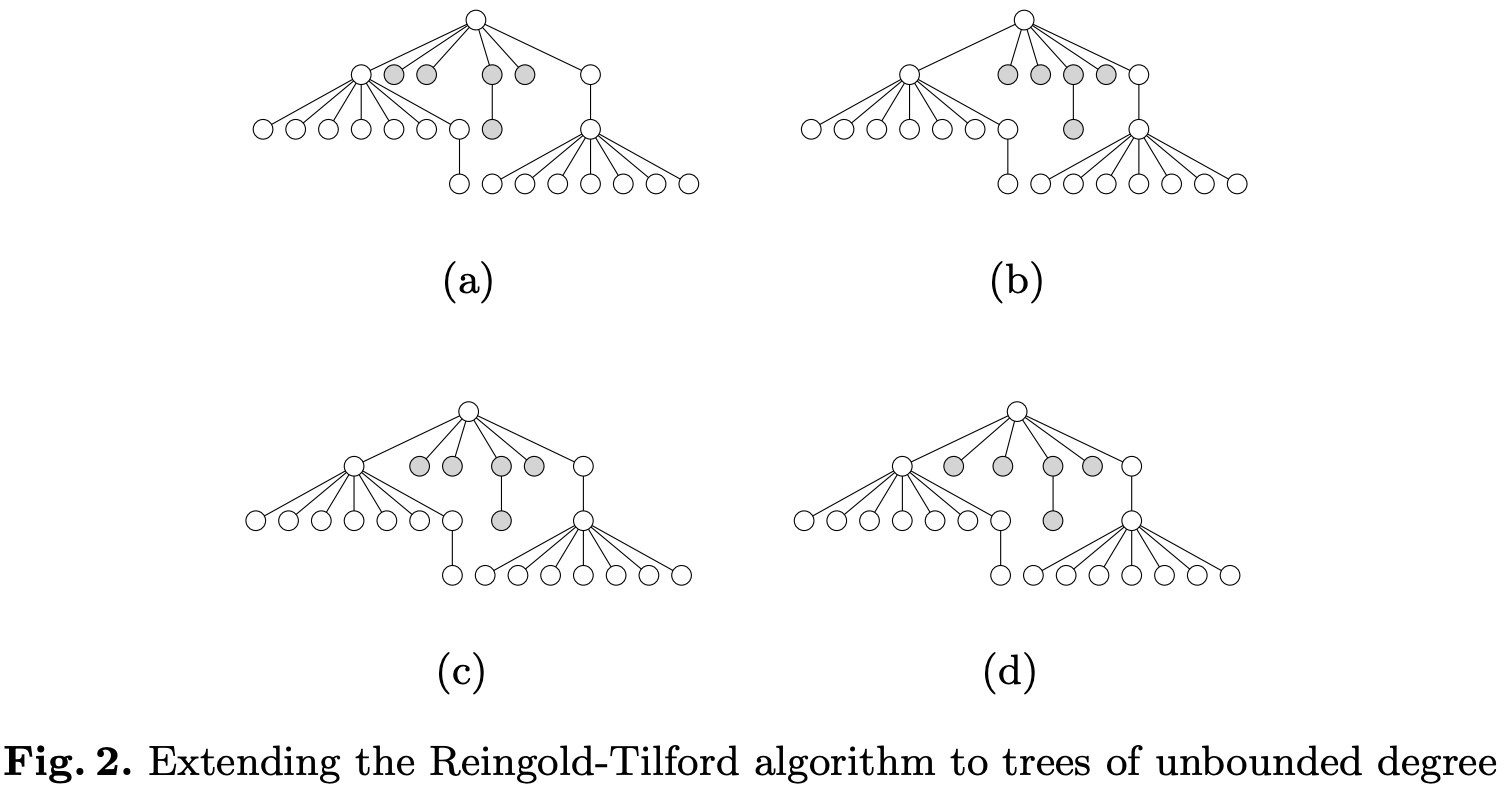
我们可以从左到右依次处理平移子树，但这样做的结果如下图 (a)，我们也可以增加一趟从右到左的遍历，但这样又会出现 (b) 的情况。我们希望实现 (d) 的效果：

source: Improving Walker’s Algorithm to Run in Linear Time

A Node-Positioning Algorithm for General Trees 提出了一种方案，值得一提的是 d3-tree 的代码结构、变量名基本复用了这篇论文。下图展示了子树添加过程中，重新布局的效果：

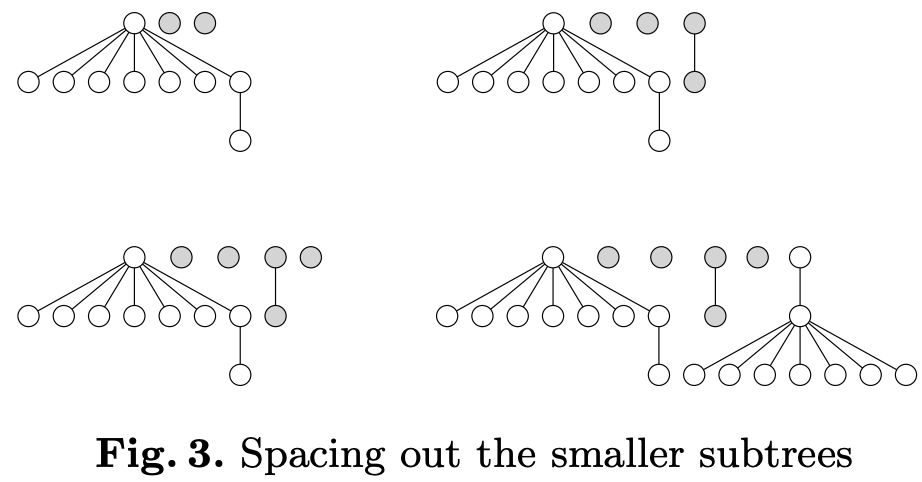
apportion 函数是整个布局核心的“子树间对齐逻辑”，它负责比较当前子树与前一个子树的轮廓；如果它们重叠，就给当前子树加一个 shift；更新 modifier 使得后代节点也随之调整；同时平滑中间的 modifier，避免“断层”。

plaintext

function apportion(v):
    leftMost = firstChild(v)
    rightMost = lastChild(v)
    defaultAncestor = leftMost

    for each child w from second to last:
        leftSibling = previousSibling(w)

        # Initialize contour pointers
        vip = w
        vim = leftSibling
        sip = vip.mod
        sim = vim.mod

        # Compare right contour of vim and left contour of vip
        while vim ≠ null and vip ≠ null:
            shift = (vim.prelim + sim + separation) - (vip.prelim + sip)

            if shift > 0:
                # Move current subtree right
                moveSubtree(ancestor(w, v, defaultAncestor), v, shift)
                sip += shift

            # move to next lower level
            vim = rightmostChild(vim)
            vip = leftmostChild(vip)

            sim += vim?.mod or 0
            sip += vip?.mod or 0

        # update default ancestor
        if rightMostChild(vim) ≠ null and leftMostChild(vip) == null:
            defaultAncestor = ancestor(w, v, defaultAncestor)

继续在节点上增加属性，存储 shift：

function TreeNode(node, i) {
    this.c = 0; // change
    this.s = 0; // shift
    this.A = null; // default ancestor
    this.a = this; // ancestor
}

其中 moveSubtree 将以 wp 为根的子树整体右移 shift 单位。

// @see https://github.com/d3/d3-hierarchy/blob/main/src/tree.js#L28C10-L28C21
function moveSubtree(wm, wp, shift) {
    var change = shift / (wp.i - wm.i);
    wp.c -= change;
    wp.s += shift;
    wm.c += change;
    wp.z += shift;
    wp.m += shift;
}

该实现的复杂度为 $O (n^{2})$ ，Improving Walker’s Algorithm to Run in Linear Time 尝试优化到 $O (n)$

如果需要在水平方向展示，只需要转置一下坐标系，将节点的 x/y 进行交换即可。

d3-flextree

上述算法有一个很明显的限制，它要求所有节点都是同样的宽高，正如很多 d3-tree 的例子都使用同样大小的圆作为节点。这里非常推荐阅读 Drawing Non-layered Tidy Trees in Linear Time 和 High-performance tidy trees visualization。

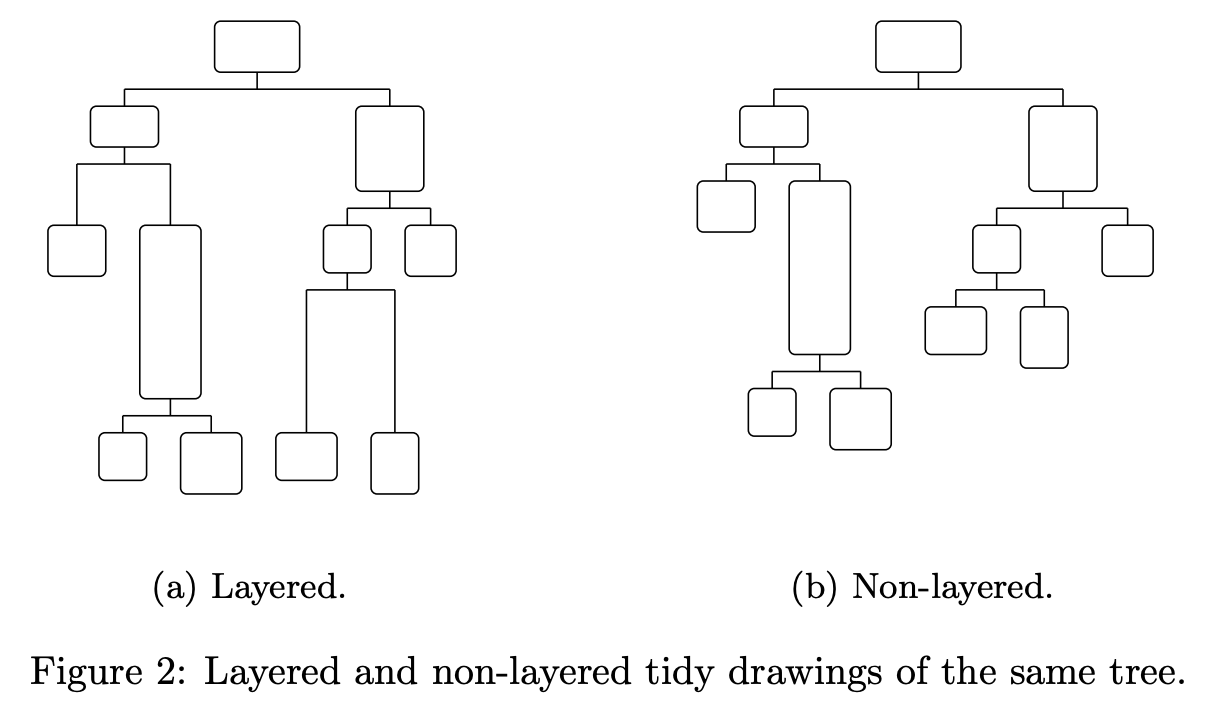
d3-flextree 正是为了解决这一问题，markmap 使用了它。

A limitation of that algorithm is that it applies to trees in which all of the nodes are the same size. This is adequate for many applications, but a more general solution, allowing variable node sizes, is often preferable.

效果如下：

@antv/hierarchy

@antv/hierarchy 中的 mindmap 算法和 mindmap-layouts 提出了以下美学要求：

根节点居中
子节点可左右分布（通常左右对称，或根据 getSide 设定）
同一层级节点按垂直方向均匀排列

它也支持定义节点尺寸，并没有使用轮廓扫描方案，大致步骤如下，整个算法复杂度为 $O (n)$ ：

第一遍：快速设置一个基础的 x 坐标。
第二遍：从下到上计算每个子树需要的垂直空间。
第三遍（调整阶段）：从上到下，利用计算好的空间信息，为所有子节点安排不重叠的 y 坐标。
第四遍：再次从下到上，根据子节点的最终布局反过来微调父节点的位置，实现垂直居中的效果。

效果如下：

[WIP] 交互

思维导图有很多特殊的交互，包括点击节点展开/收起子节点。

课程 23 - 思维导图 ​

d3-tree ​

复杂度证明 ​

扩展到 N 叉树 ​

d3-flextree ​

@antv/hierarchy ​

[WIP] 交互 ​

扩展阅读 ​