Lesson 23 - Mindmap

Many infinite canvas applications provide support for mind maps, such as miro, excalidraw, canva, xmind, etc. I really like excalidraw's categorization approach, which subdivides mind maps into three subtypes:

Spider mapping is suitable for brainstorming scenarios, extending from the central core theme like a spider web. From a rendering perspective, mermaid also provides this type.
Tree mapping
Flow map

Spider mapping	Tree mapping	Flow map

Here we only discuss the last type.

Although mind maps can vary greatly in their final presentation, from a data structure perspective, mind maps are tree structures consisting of nodes and edges. markmap and mermaid convert markdown into this structure. Trees are a special type of graph structure, and there are also some layout algorithms for directed graphs such as dagre and elkjs, but we won't consider them here.

json

{
    "id": "Modeling Methods",
    "children": [
        {
            "id": "Classification",
            "children": []
        }
    ]
}

For this type of data, d3-hierarchy provides a series of ready-to-use algorithms, and we focus only on d3-tree.

d3-tree

Let's first add two constraints that we'll later introduce how to break: the target is a binary tree, and all nodes have the same size (or no size).

d3-tree's implementation approach comes from: Tidier Drawings of Trees, which proposes several aesthetic standards based on previous research:

Aesthetic 1: Nodes at the same level of the tree should lie along a straight line, and the straight lines defining the levels should be parallel.
Aesthetic 2: A left son should be positioned to the left of its father and a right son to the right.
Aesthetic 3: A father should be centered over its sons.
Aesthetic 4: A tree and its mirror image should produce drawings that are reflections of one another; moreover, a subtree should be drawn the same way regardless of where it occurs in the tree.

The evolutionary improvement process of the first three standards can be read in Drawing Presentable Trees, which uses Python code and diagrams to show in detail the algorithmic thinking of previous papers. For example, implementing the third standard is simple: use post-order traversal and set the parent node's x-coordinate to the midpoint between the leftmost and rightmost child nodes:

// @see https://github.com/d3/d3-hierarchy/blob/main/src/tree.js#L150
var midpoint = (children[0].z + children[children.length - 1].z) / 2;

You can clearly see that it's still not symmetric enough, with an overall rightward bias, which leads to the fourth standard:

As narrowly as possible	A parent should be centered over its children

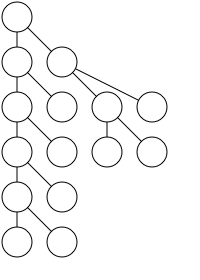The operation of centering the parent node may conflict with the position of its sibling nodes. At this point, we need to move the entire subtree, but if we use the following recursive approach, the algorithm complexity would become $O (n^{2})$ :

python

def move_right(branch, n):
    branch.x += n
    for c in branch.children:
        move_right(c, n)

At this point, we need to add a mod attribute to nodes, so that the parent centering operation can temporarily ignore conflicts and move later. This avoids recursion and brings the algorithm complexity back to $O (n)$ . We also need to add a new prelim attribute, whose name comes from: A Node-Positioning Algorithm for General Trees:

// @see https://github.com/d3/d3-hierarchy/blob/main/src/tree.js#L67
function TreeNode(node, i) {
    this._ = node; // final position: _.x
    this.parent = null;
    this.children = null;
    this.z = 0; // prelim
    this.m = 0; // mod
}

Because of using post-order traversal:

function tree(root) {
    var t = treeRoot(root);
    t.eachAfter(firstWalk);
    t.eachBefore(secondWalk);
}

In the second pre-order traversal, recursively accumulate mod to complete the rightward shift and get the final position _.x. This corresponds to the PETRIFY step in the original paper:

// @see https://github.com/d3/d3-hierarchy/blob/main/src/tree.js#L164
function secondWalk(v) {
    v._.x = v.z + v.parent.m; // final x
    v.m += v.parent.m;
}

Here we need to introduce the concept of contour. For example, the right contour of the left tree below is [1, 1, 2], and the left contour of the right tree is [1, 0, 1]. When we need to prevent these two subtrees from overlapping, we only need to compare these two contours to determine how much distance the right tree needs to move to the right. In this example, the movement distance is 2.

python

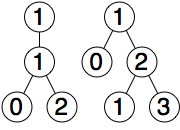
def push_right(left, right):
    wl = contour(left, lt)
    wr = contour(right, gt)
    return max(x-y for x,y in zip(wl, wr)) + 1

The algorithm for obtaining subtree contours still requires recursion, so the complexity is $O (n^{2})$ . To optimize this, the concept of thread is introduced. In the figure below, the dashed lines represent this relationship that differs from parent-child, outlining the contours of each subtree that might not actually exist:

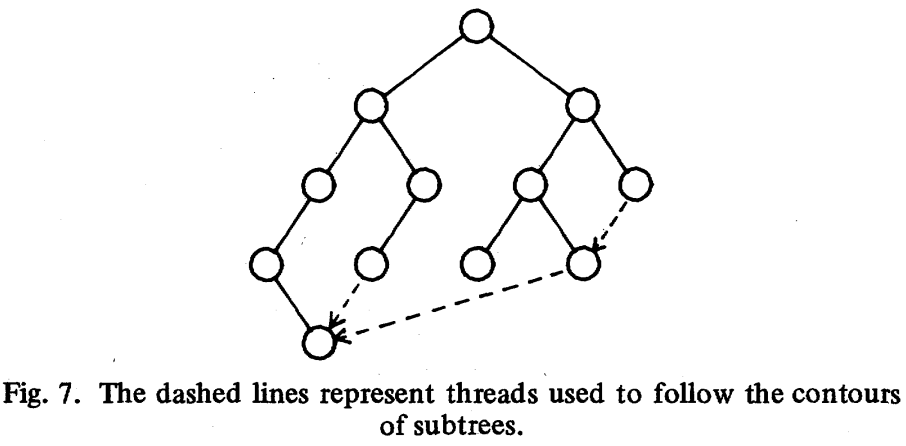
function TreeNode(node, i) {
    this.t = null; // thread
}

This way, when calculating contour, we can cross the actual hierarchical structure and directly obtain it through thread, reducing the complexity to $O (n)$ :

// @see https://github.com/d3/d3-hierarchy/blob/main/src/tree.js#L15C1-L24C2
function nextLeft(v) {
    var children = v.children;
    return children ? children[0] : v.t;
}
function nextRight(v) {
    var children = v.children;
    return children ? children[children.length - 1] : v.t;
}

Complexity Analysis

Let's review the algorithm. First, perform a post-order traversal to calculate the relative coordinates and thread of nodes, then perform a pre-order traversal to accumulate mod and determine the absolute coordinate position of each node. It's clear that each node is visited only once in these two traversals. Therefore, we only need to determine the complexity of contour scanning in the first traversal.

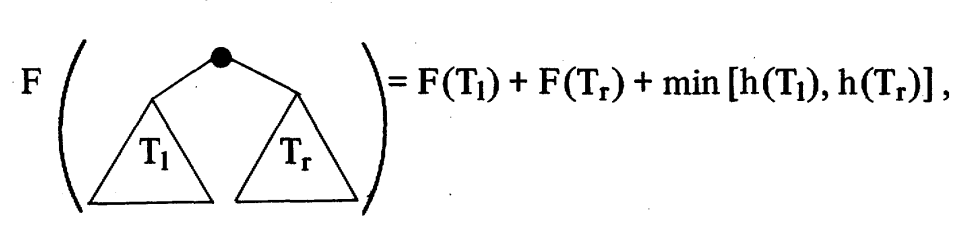
The original paper also provides a mathematical analysis of the complexity of this step. $F (T)$ represents "In the entire tree T, how many nodes does contour scanning need to visit in total?" where $h (T)$ of subtrees represents the maximum depth from root to leaf nodes, i.e., the number of path nodes - 1. It represents the worst-case access depth during contour scanning. When comparing the spacing of two contours layer by layer, once either contour reaches the bottom (no deeper layers), the scanning stops, so $m i n ()$ is used here:

Next, we only need to prove $F (T) \leq n (T)$ , where $n (T)$ represents the total number of nodes in the subtree. This confirms that the overall algorithm complexity is $O (n)$ .

The author proposes the hypothesis: $F (T) = n (T) - h (T)$ . The reasoning is that each internal node (non-leaf) participates in contour comparison at most once, while leaf nodes don't need scanning because there are no subtrees to compare. The entire tree has $n (T)$ nodes, of which at least $h (T)$ leaves are on the deepest path, so at most only $n (T) - h (T)$ nodes need to participate in contour scanning. This actually determines the upper bound of scanning access nodes, and next we only need to prove that for any tree $T$ , the number of nodes accessed by contour scanning $S c a n (T) \leq F (T)$

Using induction, it holds for $N = 0$ (no scanning needed) and $N = 1$ . Assume $S c a n (T) \leq F (T) = n (T) - h (T)$ .

According to the definition (adding the root node):

\begin{aligned} n (T) & = 1 + n (T_{l}) + n (T_{r}) \\ h (T) & = 1 + m a x (h (T_{r}), h (T_{r})) \end{aligned}

Substituting:

\begin{aligned} F (T) & = n (T) - h (T) \\ = 1 + n (T_{l}) + n (T_{r}) - [1 + m a x (h (T_{l}), h (T_{r}))] \\ = [n (T_{l}) - h_{l}] + [n (T_{r}) - h_{r}] + [h_{l} + h_{r} - m a x (h_{l}, h_{r})] \\ \geq F (T_{l}) + F (T_{r}) + m i n (h_{l}, h_{r}) \end{aligned}

Therefore: $F (T) \geq F (T_{l}) + F (T_{r}) + m i n (h (T_{l}), h (T_{r})) \geq S c a n (T)$

Extension to N-ary Trees

We can process the shifting subtrees from left to right sequentially, but this results in figure (a) below. We could also add a right-to-left traversal, but this would result in situation (b). We want to achieve the effect of (d):

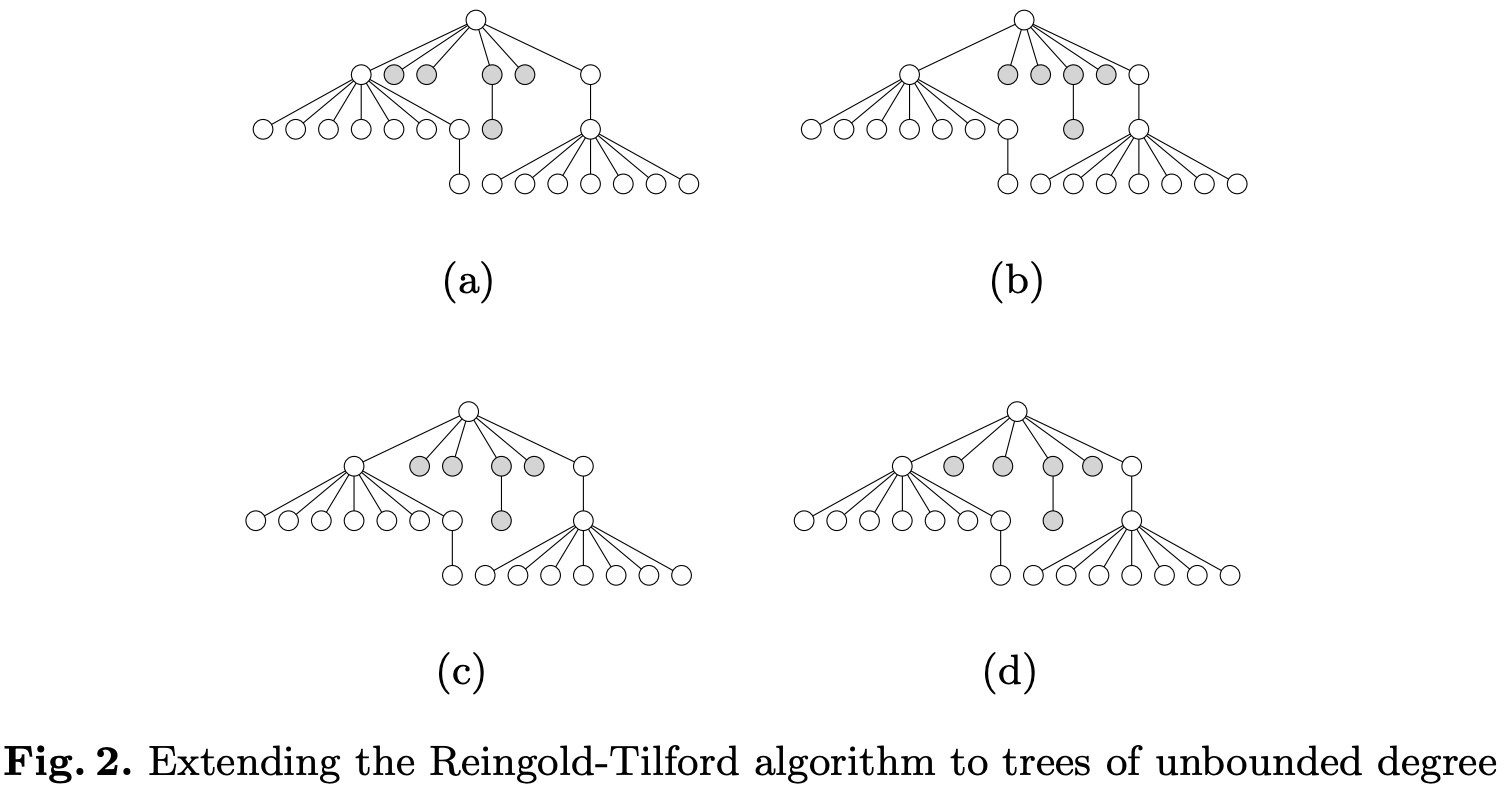
source: Improving Walker's Algorithm to Run in Linear Time

A Node-Positioning Algorithm for General Trees proposed a solution. It's worth noting that d3-tree's code structure and variable names basically reuse this paper. The figure below shows the relayout effect during the subtree addition process:

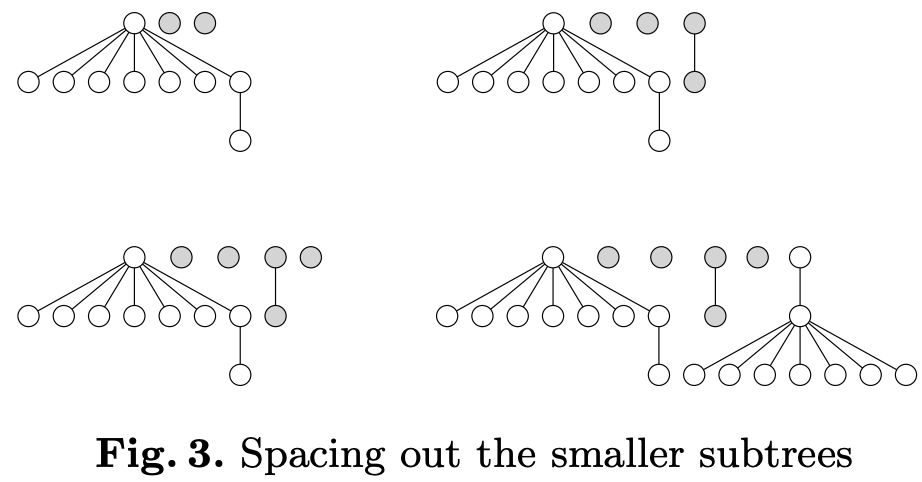
The apportion function is the core "inter-subtree alignment logic" of the entire layout. It's responsible for comparing the contours of the current subtree with the previous subtree; if they overlap, it adds a shift to the current subtree; updates the modifier so that descendant nodes also adjust accordingly; and smooths the intermediate modifiers to avoid "gaps".

plaintext

function apportion(v):
    leftMost = firstChild(v)
    rightMost = lastChild(v)
    defaultAncestor = leftMost

    for each child w from second to last:
        leftSibling = previousSibling(w)

        # Initialize contour pointers
        vip = w
        vim = leftSibling
        sip = vip.mod
        sim = vim.mod

        # Compare right contour of vim and left contour of vip
        while vim ≠ null and vip ≠ null:
            shift = (vim.prelim + sim + separation) - (vip.prelim + sip)

            if shift > 0:
                # Move current subtree right
                moveSubtree(ancestor(w, v, defaultAncestor), v, shift)
                sip += shift

            # move to next lower level
            vim = rightmostChild(vim)
            vip = leftmostChild(vip)

            sim += vim?.mod or 0
            sip += vip?.mod or 0

        # update default ancestor
        if rightMostChild(vim) ≠ null and leftMostChild(vip) == null:
            defaultAncestor = ancestor(w, v, defaultAncestor)

Continue adding attributes to nodes to store shift:

function TreeNode(node, i) {
    this.c = 0; // change
    this.s = 0; // shift
    this.A = null; // default ancestor
    this.a = this; // ancestor
}

Where moveSubtree moves the entire subtree rooted at wp to the right by shift units.

// @see https://github.com/d3/d3-hierarchy/blob/main/src/tree.js#L28C10-L28C21
function moveSubtree(wm, wp, shift) {
    var change = shift / (wp.i - wm.i);
    wp.c -= change;
    wp.s += shift;
    wm.c += change;
    wp.z += shift;
    wp.m += shift;
}

This implementation has a complexity of $O (n^{2})$ . Improving Walker's Algorithm to Run in Linear Time attempts to optimize it to $O (n)$ .

If you need to display horizontally, simply transpose the coordinate system by swapping the x/y coordinates of nodes.

d3-flextree

The above algorithm has an obvious limitation: it requires all nodes to have the same width and height, just like many d3-tree examples use circles of the same size as nodes. I highly recommend reading Drawing Non-layered Tidy Trees in Linear Time and High-performance tidy trees visualization.

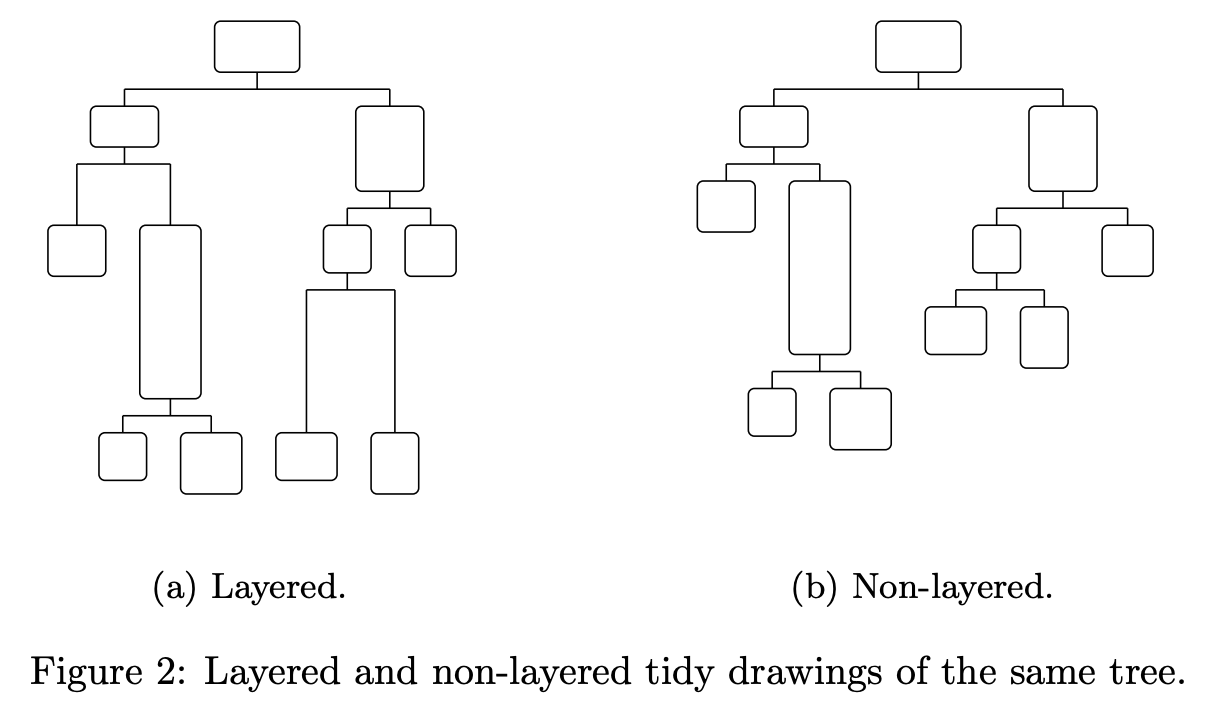
d3-flextree was created to solve this problem, and markmap uses it.

A limitation of that algorithm is that it applies to trees in which all of the nodes are the same size. This is adequate for many applications, but a more general solution, allowing variable node sizes, is often preferable.

The effect is as follows:

@antv/hierarchy

The mindmap algorithm in @antv/hierarchy and mindmap-layouts propose the following aesthetic requirements:

Root node centered
Child nodes can be distributed left and right (usually symmetrically, or set according to getSide)
Nodes at the same level are evenly arranged vertically

It also supports defining node sizes and doesn't use the contour scanning approach. The general steps are as follows, with an overall algorithm complexity of $O (n)$ :

First pass: Quickly set a basic x-coordinate.
Second pass: Calculate the vertical space needed for each subtree from bottom to top.
Third pass (adjustment phase): From top to bottom, use the calculated space information to arrange non-overlapping y-coordinates for all child nodes.
Fourth pass: Again from bottom to top, based on the final layout of child nodes, fine-tune the parent node positions to achieve vertical centering.

The effect is as follows:

[WIP] Interaction

Mind maps have many special interactions, including clicking nodes to expand/collapse child nodes.

Lesson 23 - Mindmap ​

d3-tree ​

Complexity Analysis ​

Extension to N-ary Trees ​

d3-flextree ​

@antv/hierarchy ​

[WIP] Interaction ​

Extended Reading ​