课程 5 - 绘制网格
在这节课中你将学习到以下内容:
- 绘制直线网格。使用 Line Geometry 或者屏幕空间技术。
- 绘制点网格。
- 为 Geometry 绘制 wireframe。
$button = call(() => {
const $button = document.createElement('button');
$button.textContent = 'FlyTo origin';
return $button;
});checkboardStyle = Inputs.radio(['none', 'grid', 'dots'], {
label: 'Checkboard Style',
value: 'grid',
});canvas = call(() => {
const { Canvas } = Lesson5;
return Utils.createCanvas(Canvas, 400, 400);
});call(() => {
const styles = ['none', 'grid', 'dots'];
canvas.setCheckboardStyle(styles.indexOf(checkboardStyle));
});(async () => {
const { Canvas, Circle, Group } = Lesson5;
const solarSystem = new Group();
const earthOrbit = new Group();
const moonOrbit = new Group();
const sun = new Circle({
cx: 0,
cy: 0,
r: 100,
fill: 'red',
});
const earth = new Circle({
cx: 0,
cy: 0,
r: 50,
fill: 'blue',
});
const moon = new Circle({
cx: 0,
cy: 0,
r: 25,
fill: 'yellow',
});
solarSystem.appendChild(sun);
solarSystem.appendChild(earthOrbit);
earthOrbit.appendChild(earth);
earthOrbit.appendChild(moonOrbit);
moonOrbit.appendChild(moon);
solarSystem.position.x = 200;
solarSystem.position.y = 200;
earthOrbit.position.x = 100;
moonOrbit.position.x = 100;
canvas.appendChild(solarSystem);
let id;
const animate = () => {
solarSystem.rotation += 0.01;
earthOrbit.rotation += 0.02;
canvas.render();
id = requestAnimationFrame(animate);
};
animate();
unsubscribe(() => {
cancelAnimationFrame(id);
canvas.destroy();
});
const landmark = canvas.camera.createLandmark({
x: 0,
y: 0,
zoom: 1,
rotation: 0,
});
$button.onclick = () => {
canvas.camera.gotoLandmark(landmark, {
duration: 1000,
easing: 'ease',
});
};
return canvas.getDOM();
})();在 Figma 和 FigJam 中,缩放到一定大小时会出现网格,前者是直线而后者是点状。
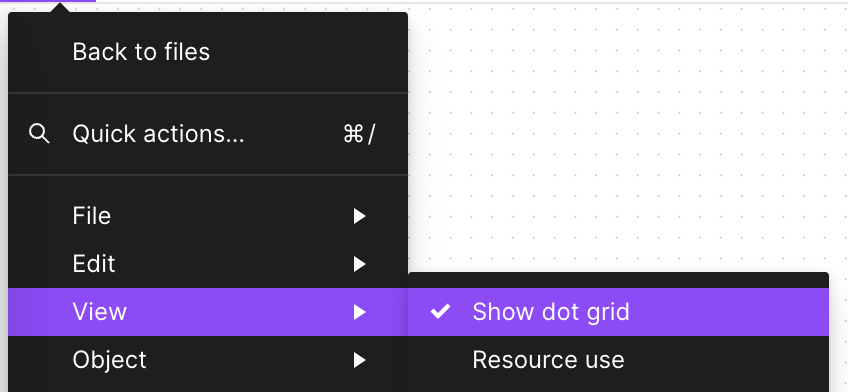
Miro 则支持在直线和点之间进行切换:
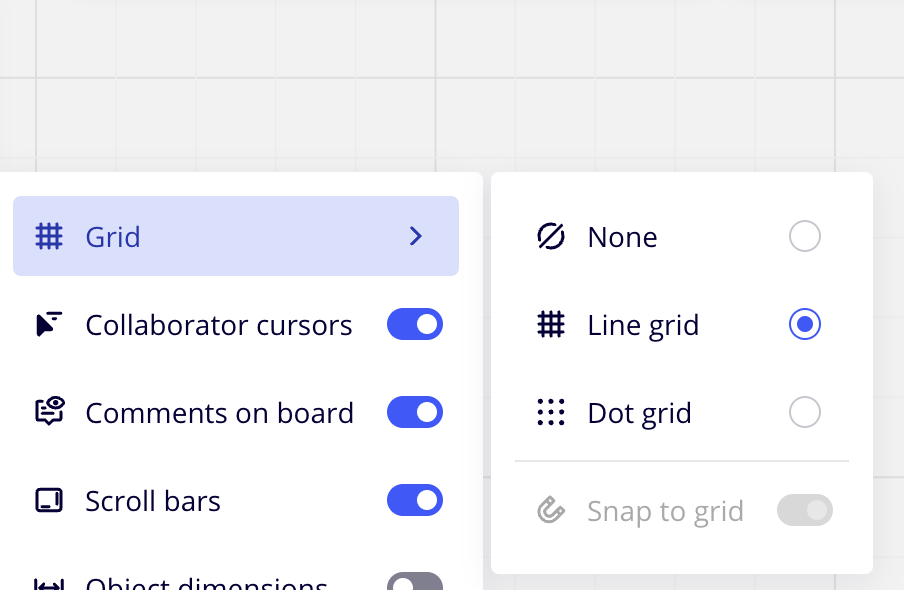
我们先来实现直线网格。
直线网格
首先网格不应该是场景图的一部分,我们不希望缩放画布时网格也跟着变大变小,但同时也要在缩放时拥有淡入淡出效果。因此我们在 beginFrame 钩子中首先渲染网格,将场景所需的信息例如相机也传递进去:
hooks.initAsync.tapPromise(async () => {
this.#grid = new Grid();
});
hooks.beginFrame.tap(() => {
this.#grid.render(
this.#device,
this.#renderPass,
this.#uniformBuffer,
camera,
);
});Line Geometry
最容易想到的思路是类似 GridHelper - Three.js 这样,根据网格尺寸创建一组线段:
// https://github.com/mrdoob/three.js/blob/master/src/helpers/GridHelper.js#L25-L37
for (var i = 0, j = 0, k = -halfSize; i <= divisions; i++, k += step) {
vertices.push(-halfSize, 0, k, halfSize, 0, k);
vertices.push(k, 0, -halfSize, k, 0, halfSize);
}
var geometry = new BufferGeometry();
geometry.addAttribute('position', new Float32BufferAttribute(vertices, 3));
geometry.addAttribute('color', new Float32BufferAttribute(colors, 3));
var material = new LineBasicMaterial({ vertexColors: VertexColors });
LineSegments.call(this, geometry, material);Figma CTO Evan 的 thetamath 项目中也是这么实现的,从水平和垂直两个方向构建网格所需的线段:
for (let x = left; x < right; x++) {
const tx = ox + (x * zoom) / step;
this.strokeLine();
}
for (let y = top; y < bottom; y++) {
const ty = oy - (y * zoom) / step;
this.strokeLine();
}如何在 WebGL 中绘制直线呢?之前我写过一篇 在 WebGL 中绘制直线,简而言之如果不考虑接头,只需要沿法线方向向两侧拉伸,使用两个三角形绘制:
thetamath 还使用了两个小技巧,首先是使用 Triangle strip,相比常规的 Triangle 能节省顶点,从 3N 减少到 N + 2,其中 N 为三角形数目:
this.#pipeline = device.createRenderPipeline({
inputLayout: this.#inputLayout,
program: this.#program,
colorAttachmentFormats: [Format.U8_RGBA_RT],
topology: PrimitiveTopology.TRIANGLE_STRIP,
});其次是将颜色存储在四个 Byte 中:
255 | (255 << 8) | (255 << 16) | (127 << 24);配合 vertexAttribPointer 声明每个分量都是 gl.UNSIGNED_BYTE 并且需要归一化:
this.#inputLayout = device.createInputLayout({
vertexBufferDescriptors: [
{
arrayStride: 4 * 5,
stepMode: VertexStepMode.VERTEX,
attributes: [
{
format: Format.F32_RGBA,
offset: 0,
shaderLocation: 0,
},
{
format: Format.U8_RGBA_NORM,
offset: 4 * 4,
shaderLocation: 1,
},
],
},
],
indexBufferFormat: null,
program: this.#program,
});看看效果:
(async () => {
const { Canvas, Circle, Group } = Lesson5;
const canvas = await Utils.createCanvas(Canvas, 400, 400);
const $canvas = canvas.getDOM();
canvas.setGridImplementation(0);
const solarSystem = new Group();
const earthOrbit = new Group();
const moonOrbit = new Group();
const sun = new Circle({
cx: 0,
cy: 0,
r: 100,
fill: 'red',
});
const earth = new Circle({
cx: 0,
cy: 0,
r: 50,
fill: 'blue',
});
const moon = new Circle({
cx: 0,
cy: 0,
r: 25,
fill: 'yellow',
});
solarSystem.appendChild(sun);
solarSystem.appendChild(earthOrbit);
earthOrbit.appendChild(earth);
earthOrbit.appendChild(moonOrbit);
moonOrbit.appendChild(moon);
solarSystem.position.x = 200;
solarSystem.position.y = 200;
earthOrbit.position.x = 100;
moonOrbit.position.x = 100;
canvas.appendChild(solarSystem);
let id;
const animate = () => {
solarSystem.rotation += 0.01;
earthOrbit.rotation += 0.02;
canvas.render();
id = requestAnimationFrame(animate);
};
animate();
unsubscribe(() => {
cancelAnimationFrame(id);
canvas.destroy();
});
return $canvas;
})();在这种方法中,画布尺寸越大、网格密度越高所需的顶点就越多,有没有办法使用更少的顶点实现呢?既然网格永远填充整个屏幕,那是否可以在屏幕空间完成呢?
Patterns in fragment shader
正如 Building Flexible and Powerful Cross-Sections with GridPaper and WebGL 一文所说:
Instead of rendering all these lines as geometry, we can use a WebGL fragment shader to generate the lines on a per-pixel basis.
在屏幕空间实现的好处是只需要一个充满屏幕的 Quad 就行了,顶点只需要四个,传入裁剪坐标系下的坐标。当然使用一个全屏幕三角形也可以,而且只需要三个顶点,这在后处理中很常见:
this.appendVertex(-1, -1);
this.appendVertex(-1, 1);
this.appendVertex(1, -1);
this.appendVertex(1, 1);这样在 Vertex Shader 中可以无需变换直接使用:
layout(location = 0) in vec4 a_Position;
void main() {
gl_Position = vec4(a_Position.xy, 0, 1);
}后续在 Fragment Shader 中绘制网格需要使用像素点在世界坐标系下的坐标。因此通过相机投影变换矩阵的逆矩阵,将裁剪坐标系下的坐标转换到世界坐标系下:
layout(std140) uniform SceneUniforms {
mat3 u_ProjectionMatrix;
mat3 u_ViewMatrix;
mat3 u_ViewProjectionInvMatrix;
};
out vec2 v_Position;
vec2 project_clipspace_to_world(vec2 p) {
return (u_ViewProjectionInvMatrix * vec3(p, 1.0)).xy;
}
void main() {
v_Position = project_clipspace_to_world(a_Position.xy);
}在 Canvas2D 和 SVG 中网格通常使用 Pattern 实现。在 Fragment Shader 中实现的基本思路也很类似,使用内置函数 fract 绘制 Pattern,将初始坐标空间放大到 n 倍,然后通过 fract 取得小数部分。这样后续只需要考虑坐标范围在 0-1 的小块即可,详见 the book of shaders - Patterns:

还是来自 Figma CTO Evan 的文章:Anti-Aliased Grid Shader
vec4 render_grid_checkerboard(vec2 coord) {
// Compute anti-aliased world-space grid lines
vec2 grid = abs(fract(coord / gridSize - 0.5) - 0.5) / fwidth(coord) * gridSize;
float line = min(grid.x, grid.y);
float alpha = 1.0 - min(line, 1.0);
}我们希望绘制两套粗细网格,其中细网格的间隔是粗网格的 1/5,同时检测当前像素点是否更靠近粗网格:
vec2 size = scale_grid_size(u_ZoomScale);
float gridSize1 = size.x;
float gridSize2 = gridSize1 / 5.0;纹理贴图
The Best Darn Grid Shader (Yet) 一文介绍了另一种基于纹理贴图的方案。特别是当我们希望线条本身也拥有透视效果时,该方案效果要好于屏幕空间的定宽网格。例如下图中右侧存在的明显“摩尔纹”现象,而左侧较远处的线条颜色也会变细、变暗。

原文中作者对定宽网格进行了一系列改进,实现了透视效果,缓解了“摩尔纹”现象等,在 Shadertoy 上的示例如下:
圆点网格
对于圆点网格,我们依旧选择在 Fragment Shader 屏幕空间中处理。当然也可以使用之前介绍过的 SDF 绘制圆的方式,但这样就需要大量顶点了。因此继续复用直线网格的 Pattern,只是这里使用 SDF 判断像素点是否在圆内,我们在第二节课中已经介绍过该方法了:
vec2 grid2 = abs(fract(coord / gridSize2 - 0.5) - 0.5) / fwidth(coord) * gridSize2;
alpha = 1.0 - smoothstep(0.0, 1.0, length(grid2) - BASE_DOT_SIZE * u_ZoomScale / zoomStep);为了支持在直线、圆点网格间切换,我们增加一个新的 Uniform 用来区分不同的网格样式:
layout(std140) uniform SceneUniforms {
mat3 u_ProjectionMatrix;
mat3 u_ViewMatrix;
mat3 u_ViewProjectionInvMatrix;
float u_ZoomScale;
float u_CheckboardStyle;
};这样在 Fragment Shader 中就可以根据这个变量绘制不同类型的网格了:
const int CHECKERBOARD_STYLE_NONE = 0;
const int CHECKERBOARD_STYLE_GRID = 1;
const int CHECKERBOARD_STYLE_DOTS = 2;
vec4 render_grid_checkerboard(vec2 coord) {
int checkboardStyle = int(floor(u_CheckboardStyle + 0.5));
if (checkboardStyle == CHECKERBOARD_STYLE_GRID) {
// 直线网格
} else if (checkboardStyle == CHECKERBOARD_STYLE_DOTS) {
// 圆点网格
}
}可以回到页面开头的例子,在不同网格间进行切换。
最后提供一个结合鼠标交互的有趣例子:How to Code a Subtle Shader Background Effect with React Three Fiber
调整亮度
在 Figma / FigJam 的 Shader 中,还计算了颜色的亮度,并根据亮度值对颜色进行调整。具体来说,它使用了一种基于亮度的颜色调整算法,旨在改善颜色的视觉效果,使得在亮度较高的背景下文字或图形更加清晰可见。
定义了一个权重向量 weights,这些权重是根据人眼对不同颜色亮度感知的非线性特性而设定的,通常用于计算 RGB 颜色空间中的亮度值。
vec3 gridColor; // 存储最终调整后的颜色值
vec3 weights = vec3(0.299, 0.587, 0.114);
float c2 = dot(rgb * rgb, weights); // 计算了RGB颜色值的加权平方和,这个值c2是颜色亮度的一个估计值
float luminance = sqrt(c2);如果亮度值大于 0.5,说明颜色本身已经比较亮,代码会计算一个调整因子 target,并用它来调整颜色值 rgb,使得颜色变得更暗一些,从而在亮背景下更易于观察。如果亮度值不大于 0.5,说明颜色本身比较暗,代码会采取另一种策略来调整颜色。首先计算一个新的亮度目标值target,然后使用 mix 函数结合 rgb 颜色和纯白色 vec3(1),根据 b 和 a 的计算结果来决定最终的颜色混合比例。这里 a 和 b 是根据原始颜色的亮度值计算得到的,用于控制颜色调整的过程。
if (luminance > 0.5) {
float target = (luminance - 0.05) / luminance;
gridColor = rgb * target;
}
else {
float target = luminance * 0.8 + 0.15;
float c1 = dot(rgb, weights);
float a = 1.0 - 2.0 * c1 + c2;
float b = c2 - c1;
gridColor = mix(rgb, vec3(1), (b + sqrt(b * b - a * (c2 - target * target))) / a);
}
rgb = mix(rgb, gridColor, gridWeight);绘制 wireframe
绘制 wireframe 也使用了类似技术,我们可以将它用于针对复杂 Geometry 的 Debug,例如后续介绍的折线。
重心坐标
思路其实十分简单,我们想在光栅化时给每个三角形描边,那么就需要知道当前 fragment 距离三角形的三边各有多远,一旦小于边框的宽度,我们就给当前 fragment 着上边框的颜色。所以问题的关键就是如何计算 fragment 距离三角形三边的距离。我们可以使用重心坐标,由于只关心当前 fragment 所在的三角形,以三个顶点构建重心坐标系,利用 fragment shader 的插值就能得到当前 fragment 对应的重心坐标。
其实在光栅化过程中,渲染管线也正是利用重心坐标作为权重来决定 fragment 的颜色,如下图所示,可以继续阅读 scratchapixel 上关于光栅化具体实现的文章:Rasterization。
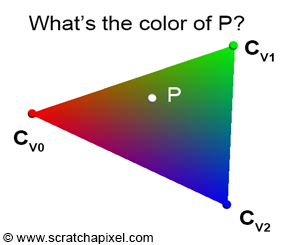
下面来看具体实现。首先给顶点传入重心坐标,我们需要保证三角形三个顶点坐标值分别是 (1,0,0) (0,1,0) 和 (0,0,1)。如果在绘制时使用的是 gl.drawArrays(),那只需要简单的按顺序依次传入三个顶点坐标,重复多次(三角形个数)就行了,我们以一个简单平面(两个三角形组成)为例:
layout(location = BARYCENTRIC) in vec3 a_Barycentric;
out vec3 v_Barycentric;
void main() {
v_Barycentric = a_Barycentric;
}然后在 fragment shader 中,当重心坐标任意一个分量小于边框宽度阈值,就可以当作边框绘制。这里用到了 glsl 内置函数 any() 和 lessThan():
in vec3 v_Barycentric;
void main() {
// 小于边框宽度
if (any(lessThan(v_Barycentric, vec3(0.1)))) {
// 边框颜色
gl_FragColor = vec4(0.0, 0.0, 0.0, 1.0);
} else {
// 填充背景颜色
gl_FragColor = vec4(0.5, 0.5, 0.5, 1.0);
}
}和之前绘制直线网格同理,我们希望线宽不要随着相机缩放而改变,应当保持定宽,因此继续使用 fwidth()
float edgeFactor() {
vec3 d = fwidth(v_Barycentric);
vec3 a3 = smoothstep(vec3(0.0), d * u_WireframeLineWidth, v_Barycentric);
return min(min(a3.x, a3.y), a3.z);
}重新分配顶点数据
之前的例子中我们在绘制时使用了 gl.drawArrays(),但如果使用的是更节省 Buffer 空间的 gl.drawElements(),也就是共享部分顶点(例如平面仅使用 4 个而非 6 个顶点),就不能简单根据顶点顺序,得依照顶点索引分配重心坐标了。但不是所有分配方式都这么简单,比如 Stack Overflow 上的这个问题:Issue with Barycentric coordinates when using shared vertices,会发现 ? 处无法分配。根本原因其实是在共享顶点的情况下,一旦给一个三角形分配好了重心坐标,与之共享一边的下一个三角形的剩余一个顶点坐标实际也已经确定了:
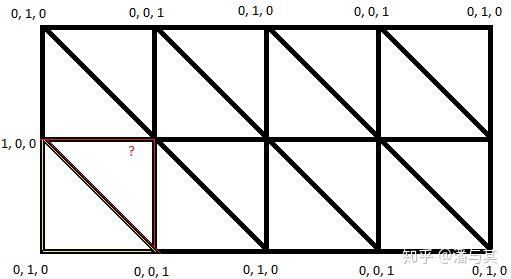
因此开启 wireframe 时,需要展开被复用的索引。以 SDF 为例,原本的 6 个顶点使用的 4 个索引 [0, 1, 2, 0, 2, 3] 将被展开为 [0, 1, 2, 3, 4, 5],同时顶点数组中的数据需要重新分配。
let cursor = 0;
const uniqueIndices = new Uint32Array(indiceNum); // 重新分配索引
for (let i = 0; i < indiceNum; i++) {
const ii = this.#indexBufferData[i];
for (let j = 0; j < bufferDatas.length; j++) {
const { arrayStride } = this.#vertexBufferDescriptors[j];
const size = arrayStride / 4;
for (let k = 0; k < size; k++) {
bufferDatas[j][cursor * size + k] =
originalVertexBuffers[j][ii * size + k]; // 重新分配顶点数据
}
}
uniqueIndices[i] = cursor;
cursor++;
}效果如下,更多图形的绘制方法后续我们会详细介绍。