课程 22 - VectorNetwork

在这节课中你将学习到以下内容：

SVG Path 的局限性
什么是 VectorNetwork？
使用 Pen 工具修改 Path
双击进入 Vector 编辑态与 Move / Bend / Cut / Fill 工具
拓扑算子：分裂边、删除顶点、Cut 断开闭合环

SVG Path 的局限性

在课程 13 - 绘制 Path & 手绘风格中我们学习了 Path 的绘制方式。Figma 也提供了 VectorPath API，它支持 SVG Path 的路径命令子集（详见：VectorPath-data）和 fillRule（Figma 中称作 windingRule）。

node.vectorPaths = [
    {
        windingRule: 'EVENODD',
        data: 'M 0 100 L 100 100 L 50 0 Z',
    },
];

那为什么还要引入 VectorNetwork API 呢？原因在于 SVG Path 存在一些天然的局限性。The Engineering behind Figma's Vector Networks 一文很直观地展示了这一点。下面的图形是无法仅仅使用一个 Path 描述的：

Not valid paths

只能通过拆分成多个 Path 描述，虽然可行，但在编辑场景下无法实现某些很符合直觉的操作。例如拖动左下的中心顶点时，只有一个顶点会跟随，因为它由两个独立的 Path 组成：

Multiple paths are used to create more complex shapes

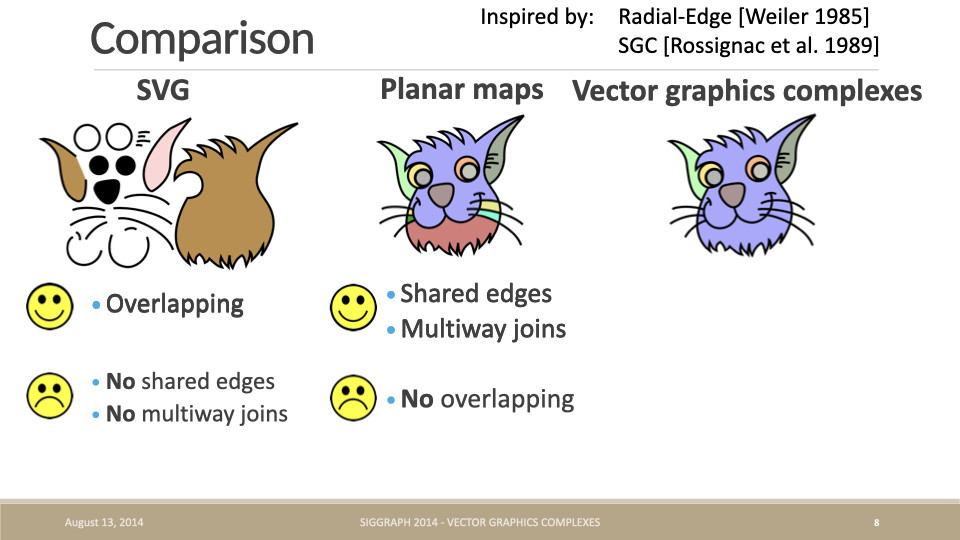
除了顶点无法拥有超过 2 条边，边也无法共享。Vector Graphics Complexes 的原始论文和 PPT 中对比了 SVG 和 Planar maps，两者都无法支持重叠、共享顶点和边这些特性，这才引出了一种新的几何表达（下文简称为 VGC）：

vpaint 就是基于 VGC 实现的，可以看到完成合并点和边的操作之后，编辑中的联动效果是多么自然：

或者使用 The Engineering behind Figma's Vector Networks 一文中拖拽立方体一条边的例子：

Dragging an edge of cube

鼠标双击进入编辑，可以拖拽立方体的任意一条边：

值得一提的是，Discussion in HN 中提到了 VGC 和 Figma 的 VectorNetwork 之间奇妙的相似程度，考虑到两者几乎处于同一时期开始探索，在某种程度上算殊途同归，因此下文就使用 VectorNetwork 这一名词了。

CEO of Figma here. Most of the original insights around vector networks were in 2013, though we continued to polish the implementation over time. We didn't exit stealth and ship the closed beta of Figma until December 2015 which is why there isn't blog content before then. At first glance, this thesis looks super neat! I'm excited to check it out! I don't believe I've seen it before which is surprising given the overlap.

下面我们来看 VectorNetwork 是如何定义的。

VectorNetwork 的拓扑定义

VectorNetwork / VGC 的定义相比 Path 路径要复杂得多，其数据结构是一个图，由顶点、边和面（填充区域）组成，下图来自 Vector Graphics Complexes 原始论文。它不需要特定的方向或闭合于起始点，允许多个路径在同一对象内向任何方向分支，这使得创建复杂形状更加迅速高效。

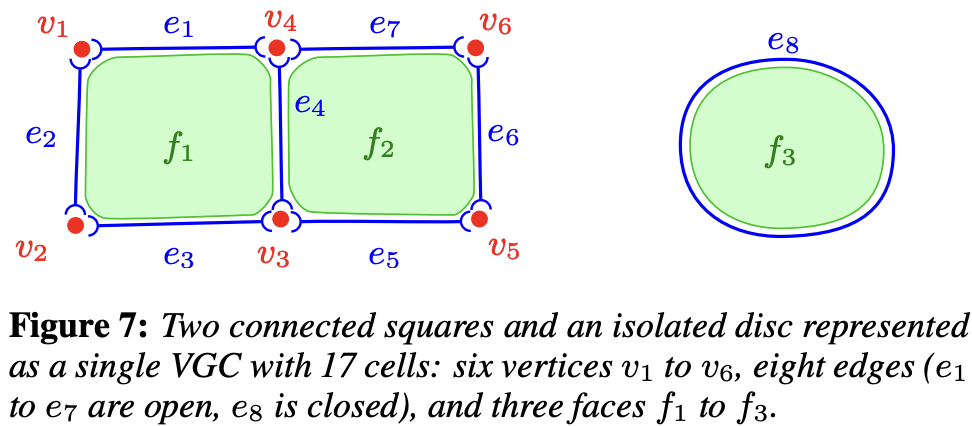
这里仅讨论拓扑定义，其他绘图属性和 Path 可以保持一致：

On top of this core structure, more drawing attributes can be added for fine control on rendering. For instance, we added vertex radius, variable edge width, cell color (possibly transparent), and edge junctions style (mitre join or bevel join).

顶点很好理解，在 VGC 中的边由一组 start 和 end 的顶点索引组成，两者重合时为自环。

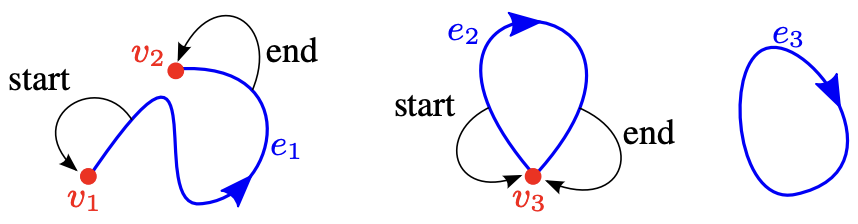
而填充区域由一组顶点组成的闭合环路定义。在 VGC 中使用一组 halfedge 定义：

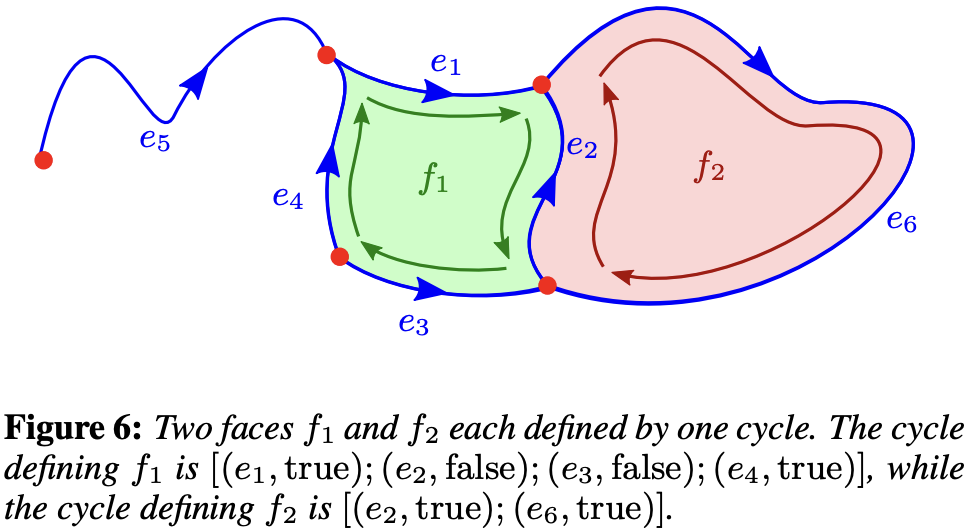
下面三角形的例子来自 VectorNetwork API，可以看到和 VGC 基本一致，只是填充区域由顶点索引和 fillRule 定义。其他非几何定义属性例如 strokeCap 和 Path 保持一致：

node.vectorNetwork = {
    // The vertices of the triangle
    vertices: [
        { x: 0, y: 100 },
        { x: 100, y: 100 },
        { x: 50, y: 0 },
    ],

    // The edges of the triangle. 'start' and 'end' refer to indices in the vertices array.
    segments: [
        {
            start: 0,
            tangentStart: { x: 0, y: 0 }, // optional
            end: 1,
            tangentEnd: { x: 0, y: 0 }, // optional
        },
        {
            start: 1,
            end: 2,
        },
        {
            start: 2,
            end: 0,
        },
    ],

    // The loop that forms the triangle. Each loop is a
    // sequence of indices into the segments array.
    regions: [{ windingRule: 'NONZERO', loops: [[0, 1, 2]] }],
};

按 Figma 约定用三次贝塞尔 —— (P_0=) 起点，(P_3=) 终点，(P_1=P_0+) tangentStart，(P_2=P_3+) tangentEnd；直线（两端控制点与锚点重合）用 2 点；否则用 CubicBezierCurve.getPoints，分段数由弦长与控制多边形长度估算（8 ～ 64）

在编辑场景下，顶点和边由用户定义，而填充区域需要系统自动计算。那如何找到这些填充区域呢？

Filling

在 click to fill 这样的操作中，需要找到顶点组成的最小环路。

Source: https://www.figma.com/blog/introducing-vector-networks/

我们把 VectorNetwork 看作平面图，每条 segment 拆成两条有向半边（half-edge）。在每个顶点处把出边按极角排序，沿着「下一条半边」（相对于反向边最靠近顺时针方向的那条出边）遍历就能枚举出所有最小面（face）。包含点击位置且面积最小的那个面即为目标填充区域，把它的有序 segment 下标序列写入 VectorRegion.loops 即可复用上文的填充三角化。

export function findRegionLoopAtPoint(
    vertices: VectorVertexLike[],
    segments: VectorSegmentLike[],
    point: [number, number],
): number[] | null;

数值稳健性：共线、重合顶点与自环都需要 EPS 容差与退化处理；外侧无界面（outer face）在该遍历下有符号面积为正，需要跳过。

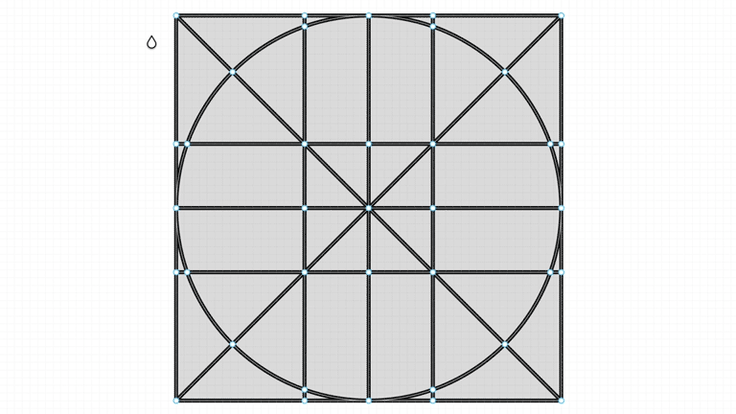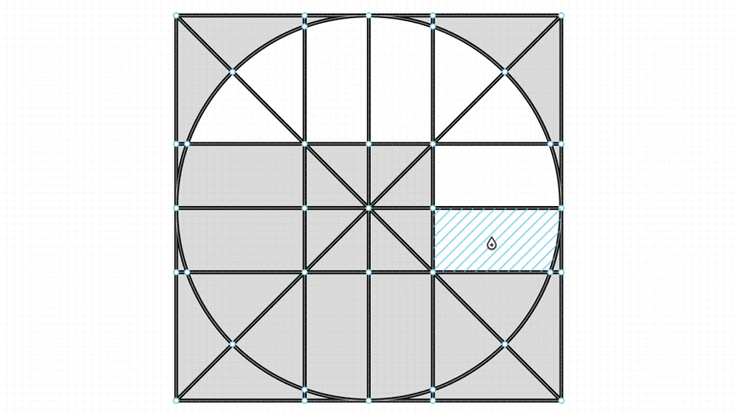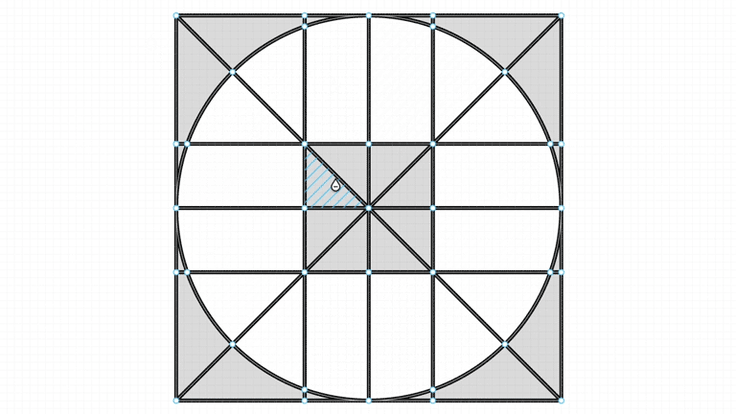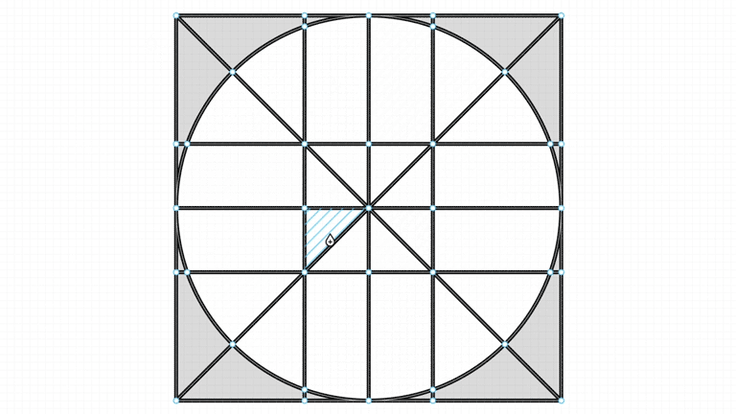
转换方法

参考 figma-fill-rule-editor，我们给出如下类型定义：

export class VectorNetwork {
    @field.object declare vertices: VectorVertex[];
    @field.object declare segments: VectorSegment[];
    @field.object declare regions?: VectorRegion[];
}

interface VectorVertex {
    x: number;
    y: number;
    strokeLinecap?: Stroke['linecap'];
    strokeLinejoin?: Stroke['linejoin'];
    cornerRadius?: number;
    handleMirroring?: HandleMirroring;
}

interface VectorSegment {
    start: number;
    end: number;
    tangentStart?: VectorVertex;
    tangentEnd?: VectorVertex;
}

interface VectorRegion {
    fillRule: CanvasFillRule;
    loops: ReadonlyArray<ReadonlyArray<number>>;
}

Polyline 是最容易转换成 VectorNetwork 的图形：

class VectorNetwork {
    static fromEntity(entity: Entity): VectorNetwork {
        if (entity.has(Polyline)) {
            const { points } = entity.read(Polyline);
            const vertices: VectorVertex[] = points.map(([x, y]) => ({ x, y }));
            const segments: VectorSegment[] = points.slice(1).map((_, i) => ({
                start: i,
                end: i + 1,
            }));

            return { vertices, segments };
        }
    }
}

[Path] 的转换更复杂一些，需要把 SVG path 命令规范化（path2Absolute）后逐段解析：M/L/H/V 生成直线 segment；C/S/Q/T 生成 cubic（Q/T 先升阶为三次），并按 Figma 约定把绝对控制点换算成相对切线 tangentStart = P1 - P0、tangentEnd = P2 - P3；S/T 需要维护上一段控制点做反射；Z 闭合时若末点与起点重合则复用起点顶点，避免重复，并为闭合子路径产出 region loop。该逻辑实现在纯函数 pathToVectorNetwork(d, fillRule) 中，fromEntity 在 entity.has(Path) 时调用它。

三角化

Stroke

我们需要将邻接边转换成折线后，使用课程 12 - 绘制折线中介绍的方法渲染。

为每个顶点维护邻接边
在未使用的边上迭代，从一条边出发先向前、再向后延伸，仅在「当前顶点只剩一条未使用边」时继续，从而在 degree 为 2 的顶点合并为一条折线（用 join 代替 cap）
分叉处 (degree ≥ 3) 停止，子路径之间用 NaN 分隔

对于每一条邻接边：

按 Figma 约定用三次贝塞尔，它的 P_0 就是起点，P_3 就是终点，P_1 = P_0 + tangentStart，P_2 = P_3 + tangentEnd
直线（两端控制点与锚点重合）用 2 点
否则用 CubicBezierCurve.getPoints，分段数由弦长与控制多边形长度估算

function tessellateVectorSegment(
    vertices: VectorVertexLike[],
    seg: VectorSegmentLike,
): number[] {
    const a = vertices[seg.start];
    const b = vertices[seg.end];
    const p0 = vec2.fromValues(a.x, a.y);
    const p3 = vec2.fromValues(b.x, b.y);

    const ts = seg.tangentStart;
    const te = seg.tangentEnd;
    const p1 = vec2.create();
    const p2 = vec2.create();
    vec2.add(p1, p0, vec2.fromValues(ts?.x ?? 0, ts?.y ?? 0));
    vec2.add(p2, p3, vec2.fromValues(te?.x ?? 0, te?.y ?? 0));
}

Fill

按 Figma 的 loops（有序 segment 下标）走一圈，用与描边相同的 tessellateVectorSegment 把每条边（含 cubic）细分，按拓扑方向拼接，去掉重复点并闭合。

对每个 region 的每个 loop 生成一条闭合轮廓
nonzero（或 Figma 的 windingRule: 'NONZERO'）：用 triangulate（libtess）的非零绕数规则，同时处理区域中的所有轮廓，支持不连通区域与嵌套孔洞
evenodd（或 EVENODD）：用 triangulate（libtess）
多个 region 依次三角化后，把顶点与索引拼到同一张 mesh 上（vOffset 累加）

点击填充区域

双击 VectorNetwork 进入编辑，选择 Fill 工具。鼠标悬停时预览最小封闭面，点击添加填充，再次点击取消；一次点击对应一次撤销记录。拖动、指针取消和多指缩放不会提交填充。切换工具、按 Esc、点击图形外的空白或销毁画布会清理预览。

下面的立方体已进入 Fill 模式。将鼠标移到正面、顶面或右侧面上预览，点击即可填色。试着填充两个相邻的面，再次点击其中一个面：只有这个面的填充会被清除。使用画布中的 撤销 / 重做 按钮可以逐步回退或恢复操作。

在 Fill 模式下，点击工具按钮旁的颜色色块即可打开取色器。先选择颜色或输入色值，再点击要填充的面。修改颜色也会更新这个网络中所有已填充的面，颜色修改支持撤销。目前各个面共用同一套填充样式。

findVectorNetworkFaces 枚举有方向的半边环，并将不连通内层组件的外边界作为所属面的孔洞。预览和新建区域使用 evenodd，因此孔洞不依赖边的存储方向。已有 nonzero / evenodd 填充会按实际覆盖范围转换为最小面，取消其中一个面时保留其他面的填充。

所有面共用节点的 fills。对只有描边的网络首次填充时，使用钢笔配置中的可见填充；若没有配置，则使用蓝色。预览位于临时 SVG 覆盖层，不进入文档、导出或撤销记录。命中测试使用局部坐标，支持旋转、镜像和缩放。

Fill 会先在临时几何上把交点拆成共享顶点，再查找最小封闭面；悬停不修改文档，首次点击填充时才把拓扑与填充一起提交，一次撤销即可恢复。每个面独立的颜色仍属于后续扩展。

使用钢笔绘制

选择 Vector Network 钢笔。单击放置角点，拖动放置平滑点。首个锚点在第一条边提交前只作为临时预览显示，放弃单个点不会在文档中留下空节点。

拖动向量定义新锚点的出射控制柄，入射控制柄取相反方向；下一条边沿用该向量作为 tangentStart。橡皮筋预览与实际提交共用相同的三次贝塞尔控制点计算，首个锚点也支持拖动设置切线。拖动时同时显示控制柄辅助线。

在已有锚点的 10 个视口像素范围内单击，可闭合网络并返回选择工具。吸附使用按下位置，拖动闭合点的控制柄不会新增顶点。闭合后自动识别区域，并采用钢笔配置的填充；默认仅描边样式仍需使用 Fill 才会上色。单击当前活动锚点，或按 Enter / Esc，可结束开放路径；尚未完成的拖动会被丢弃。

每条提交的边对应一次撤销。指针取消、离开画布、切换工具都会放弃当前手势，已提交的边保持不变。绘制中撤销或收到外部几何更新后会清除续画点，避免连接到失效的顶点。预览保存在所属画布的临时 SVG 层，不进入保存数据、历史记录或导出；画布销毁时同步清理。

从已有网络续画

选中一个 VectorNetwork 后切换到钢笔，靠近已有顶点时会显示吸附提示。点击该顶点作为起点，再点击或拖动下一个锚点，就会在同一个网络中添加边；既可从端点延长，也可从共享顶点建立分支。选择起点不会修改文档，提交每条新边才产生一条撤销记录。点击远离顶点的空白则新建独立网络。

续画支持旋转、非等比缩放和镜像，曲线预览与提交使用同一组控制点。已有边的切线、填充和孔洞会被保留；新增封闭面可用 Fill 工具填充。连接到已有顶点后结束本次绘制，重复连接相同的边不会创建副本。锁定、隐藏或变换不可逆的节点不能续画。取消、切换工具或绘制期间撤销会丢弃尚未提交的边，保留已完成的编辑。

Bending

Bend 支持直接拖动边上的任意内部位置：端点保持原位，被按住的曲线位置跟随鼠标。直线会转换为三次贝塞尔曲线，已有曲线从按下时的快照计算控制点，避免连续拖动造成累积偏移。旋转、镜像和非等比缩放下采用同样的屏幕空间命中逻辑。

对于参数 t，两控制点的权重为 a = 3(1-t)²t、b = 3(1-t)t²。指针位移为 Δ 时，控制点分别移动 aΔ/(a²+b²) 和 bΔ/(a²+b²)，在满足抓取位置跟随指针的前提下，最小化控制点位移。直接拖边会解除其端点的控制柄联动，其他边的控制点保持不变。接近端点的位置由锚点或手柄交互接管。

双击矢量网络，选择 Bend，再单击锚点显示控制柄。对于恰有两个关联边端点的锚点，Handle coupling 提供三种模式：

Independent：独立移动控制柄，不影响另一侧。
Align angles：保持两侧方向相反，另一侧的长度不变。
Mirror angle and length：保持两侧方向相反且长度相等。

切换模式会以第一个非零控制柄为基准立即对齐。拖动时按住 Alt 可以解除联动，松开后该锚点继续保持独立模式。连接三条或更多边的分叉点始终独立编辑；自环贡献两个关联端点。零长度控制柄没有方向，因此仅角度联动会先保留另一侧，直到拖出的控制柄重新具有方向。

直线也会显示指向另一端点的临时手柄，拖动后才创建实际的贝塞尔控制点。这些提示不会提前改变保存的几何。每次完成拖动或切换联动模式各占一个撤销步骤。Esc、指针取消、离开画布或切换工具会取消尚未完成的拖动并恢复原几何。调整曲线边界时，旋转、镜像和缩放后的锚点位置也保持不变。

下文来自 Introducing Vector Networks - Bending，对于贝塞尔曲线的编辑，在 Path 和 VectorNetwork 中都是通用的：

Vector graphics today are based on cubic bezier splines, which are curves with two extra points called control handles that are positioned away from the curve itself and that control how much it bends, sort of like how a magnet might bend a wire towards it. Changing the shape of a curve involves dragging a control handle off in space instead of dragging the curve directly.

Control points in edge

在 VectorNetwork 的边定义中，使用 tangentStart 和 tangentEnd 可以定义三阶贝塞尔曲线的两个控制点，当两者为 [0, 0] 时退化为直线。

也可以在 Konva 的 How to modify line points with anchors? 在线例子或者 bezierjs 中体验。

双击进入编辑态、Move / Bend / Cut / Fill 工具条与 midpoint 插入等交互见下文进入编辑态与工具条。

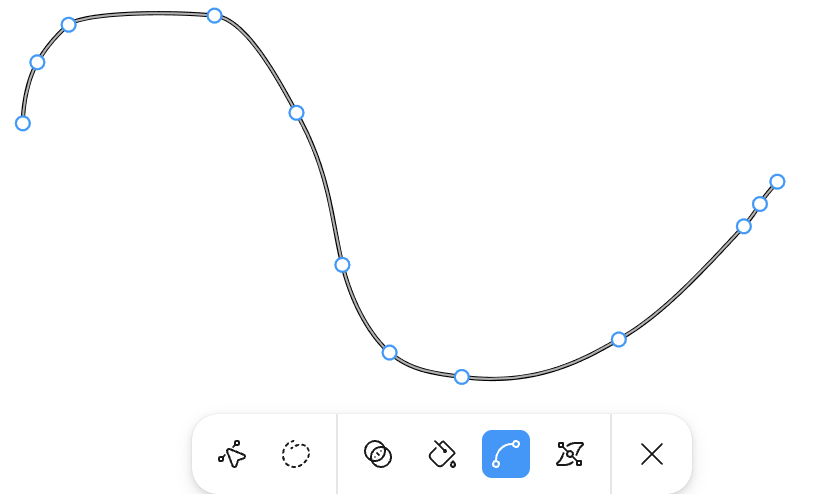
export enum Pen {
    SELECT = 'select',
    HAND = 'hand',
    VECTOR_NETWORK = 'vector-network', 
}

有别于课程 21 - Transformer 中基于 OBB 的实现：

编辑态下拖拽 VectorSegment 同时移动该边的两个端点；与它们共享顶点的相邻边自然联动
拖拽 VectorVertex 只移动该顶点本身，所有共享它的 segment 自然联动——这是 Vector Network 相较 Path 的核心价值。拖拽产生的新坐标通过统一写回入口 API.updateNodeVectorNetwork(node, vectorNetwork) 落到实体的 VectorNetwork 组件，并触发重新三角化与历史记录（undo/redo）。

// packages/ecs/src/systems/Select.ts
// 在 handleControlPointMoving 中，针对 vector-network 节点：
// 1. 读取 VectorNetwork 组件，用 GlobalTransform 的逆变换把指针坐标转回局部坐标
// 2. 更新 vertices[activeIndex].x/y
// 3. 调用 api.updateNodeVectorNetwork 写回

写回时复用 VectorNetwork.getGeometryBounds 重算几何包围盒，并将顶点整体平移 -minX/-minY，使包围盒左上角归一化到局部 (0, 0)。补偿到 node.x/y 的偏移先经过节点的缩放和旋转，转换到父节点坐标系，因此重算边界不会改变锚点的世界位置。相对锚点定义的切线向量无需平移。

进入编辑态与工具条

参考 Figma 的 Edit vector layers，双击 vector-network 节点进入顶点编辑态：为实体添加 Editable.isEditing = true，并显示底部居中的 Move / Bend / Cut / Fill 工具条（VectorNetworkEditMode，见 context-vector-network-edit-bar.ts）。退出编辑（工具条关闭按钮、Esc 或点击画布空白）时写回 isEditing: false，RenderTransformer 会隐藏所有编辑锚点（顶点、线段 midpoint、切线手柄）。

模式	交互
Move	拖拽顶点；hover 线段显示 midpoint，点击插入新顶点
Bend	直接拖动边弯曲，或选中顶点调整支持三种联动模式的切线手柄
Cut	与 Move 相同可在线段 midpoint 插入顶点；点击顶点在 cut 点断开拓扑并自动切回 Move，便于拖拽分离
Fill	悬停预览封闭面；点击切换该面的填充，保留孔洞及其他面

锚点的 hover 高亮与选中分离：Transformable.hoveredControlPointIndex 随指针移开消失，selectedControlPointIndex 在点击后保持，直到点击空白或图形内部取消。

Move：线段 midpoint 插入顶点

hover 某条 segment 时在曲线中点（t = 0.5，cubic 边取曲线上的点）渲染 midpoint 锚点。点击后调用 splitSegmentAt（见 Creation & delete）分裂该边并写回 network。相关逻辑在 Select.insertControlPointFromMidpoint 与 RenderTransformer.findHoveredVectorNetworkSegmentIndex（viewport 空间到局部曲线的距离检测）。

Move 支持拖动单个顶点或整条边；移动整条边时同时移动两端顶点，并保留切线。旋转、缩放或镜像后的节点也使用按下时的坐标系计算拖动，避免包围盒更新导致位置漂移。顶点拖到另一顶点附近时吸附，松开后合并。Esc、指针取消或切换工具会还原整个手势，包括刚插入的中点。Cut 在点击时提交断开，松开不会重新焊接。删除作用于已选中的顶点，鼠标移开后仍可操作。

拖动中的几何属于未提交手势。执行撤销或重做之前，先恢复该手势的起始几何，再应用历史记录，避免混用拖动中的包围盒与已提交的顶点。若外部更新已替换几何或变换，则直接丢弃旧手势，保留最新文档；随后移动、松开或按 Esc 都不会写回旧快照。仅改变颜色等样式不会打断拖动，取消几何时也会保留新样式。拖动中按 Delete 会先取消未完成的移动，再删除选中的原始顶点；若目标是刚插入的中点，则仅取消本次插入。

Topological operators

交点自动拆分

钢笔提交新边、完成 Move 或 Bend 拖动时，会把同一网络内的横向交叉和 T 型连接拆成共享顶点，支持直线、三次贝塞尔曲线、多交点及单条曲线的自交。拆分使用 de Casteljau 算法，保留曲线形状，并按原边界遍历方向改写区域与孔洞引用。已有顶点索引保持稳定，钢笔可继续从刚点击的端点续画。

拖动期间不拆分，松开后与形状变化一起提交；取消拖动不会留下交点，撤销和重做覆盖整个操作。也可调用 splitVectorNetworkIntersections(network) 显式整理导入的几何。算法采用自适应细分和数值迭代，暂不处理相切接触、重叠边的布尔合并或不同节点之间的连接。仅端点重合的边不会自动焊接，以保留 Cut 的结果。

Figma 支持 Boolean operations，例如 union

source: https://help.figma.com/hc/en-us/articles/360039957534-Boolean-operations

也许可以参考 Paper.js 的实现。

Creation & delete

Delete and Heal for Vector Networks

新增顶点：在某条 segment 的参数 t 处把它分裂成两段并插入新顶点（cubic 边用 de Casteljau 细分以保持曲线形状），而不是简单地往 points 数组里 splice：

export function splitSegmentAt(
    network: VectorNetworkData,
    segIdx: number,
    t: number,
): number; // 原地更新 network，返回新顶点索引

删除顶点：移除该顶点及其关联边后，对 degree==2 的相邻顶点执行「heal」——把它的两条边合并为一条，从而保持路径连通（对齐 Figma 的 Delete and Heal）。编辑态下按 Delete / Backspace 触发：

export function deleteVertex(
    network: VectorNetworkData,
    vertexIdx: number,
): VectorNetworkData;

删除、断开和合并返回新的网络；splitSegmentAt 原地更新传入的网络副本并返回新顶点索引。这些算子位于 packages/ecs/src/utils/vector-network-topology.ts，方便单测且与渲染解耦；编辑系统拿到结果后再通过 API.updateNodeVectorNetwork 统一写回。

曲线节点的 Heal 优先恢复原曲线的细分；一般曲线使用带误差上界检查的拟合，默认容差为控制点包围范围的 5%，可通过 maxError 指定局部坐标容差。超过容差时保留原网络。Shift + Delete / Backspace 仅删除节点和关联边，不执行 Heal。分割与编辑会按环的遍历方向更新边索引，保留有效区域。

Glue & unglue

在 Move 模式下选中顶点，点击工具栏的 Glue / Unglue（链条图标）。打开面板后，画布会显示顶点编号 V1、V2…… 和关联边编号 E1、E2……。

Glue：选择目标顶点并确认，将当前顶点移动到目标位置，合并它们的连接关系。保留不同的曲线和曲线自环，合并几何相同的重复边。
Unglue：勾选要拆开的边端点并确认，在原位置创建新顶点，仅将勾选的端点连接到副本。副本会自动选中，可以直接拖走。至少保留一个端点连接到原顶点；自环的起点和终点可以分别选择。

试着选中立方体正面右上角的交汇点，打开 Glue / Unglue，拆开 E7 · Start。将选中的副本拖走，再用 Glue 选择 V3，就能把它接回原顶点。

预览不修改文档，点击 Cancel 可以取消；外部几何更新、撤销或退出编辑会使待执行操作失效。每次确认对应一次撤销。Unglue 保持曲线形状及仍然闭合的区域；若外边界或孔洞被打开，会移除整个受影响的填充区域。Glue 恢复连接关系，但不会自动恢复已移除的填充：可以重新使用 Fill，或通过撤销恢复之前的完整状态。

glueVertices(network, source, target) 和 unglueVertex(network, vertex, endpoints) 返回 VectorTopologyResult：失败时包含原因，成功时包含新网络、顶点与边的索引映射，以及操作后选中的顶点索引。端点使用 { segmentIndex, end: 'start' | 'end' } 表示，API 索引从 0 开始。输入不会被修改。第一阶段支持同一网络内的顶点操作，共享边和面的操作见下文。

共享边的 Glue / Unglue

在 Move 中选中边的一个端点，打开 Glue / Unglue，将 Topology target 切换为 Edges。选择 Source edge 后，画布会标注相关区域 R1、R2……；勾选的区域会高亮。边界引用以 R（区域）· L（边界环）· 环内位置 编号，编号均从 1 开始。

下面的立方体已填充三个面。选中正面右上角 V3，选择 Unglue edge → E7，勾选 R2 · L1 · 4（顶面）并确认。顶面的这条边会改用副本 E10，右面仍使用 E7。操作后自动进入 Bend，拖动这条斜边的中部，只会弯曲副本及顶面边界；两个端点仍然共享。若要编辑重合的原边，可以返回 Move，在 Edges 面板选中 E7，然后点击 Bend selected edge。

试完 Bend 后先撤销这次弯曲，让两条边重新重合，再切回 Move 并选中 V3。在 Edges 面板选择 Glue edges，将 E10 合并到 E7。Glue 支持相反的边存储方向，也会焊接位置重合但索引不同的端点；只移除选中的源边，不会顺带合并其他重复边。曲线及其控制点不匹配、端点关系不兼容，两条边出现在同一边界环中，或合并会改变 nonzero 填充的部分边界绕向时，操作会被拒绝。

Unglue 保留曲线形状、端点和全部区域，包括孔洞；它只把选中的边界引用改到副本。必须保留至少一个引用在原边上。当前区域数据记录的是填充边界，因此边须被至少两个已填充区域边界引用；未填充的相邻面请先用 Fill 填充。已有宽区域可通过 Fill 操作拆分为独立面域。重合边尚未分开时，优先使用 Bend 或 Glue；Fill 和面级 Cut / Uncut 的面识别仍以平面嵌入为前提。每次 Glue / Unglue 对应一条历史记录，选择预览和 Bend selected edge 本身不写入历史。

纯函数 vectorEdgeUses(network, edge) 返回 { regionIndex, loopIndex, offset } 引用列表；unglueVectorNetworkEdge(network, edge, uses) 和 glueVectorNetworkEdges(network, source, target) 返回 VectorEdgeTopologyResult，包含新网络、顶点/边索引映射及选中的边，或明确的失败原因。API 索引从 0 开始，输入不会被修改。

Cut & uncut

切分与合并面

在 Move 模式选中顶点，点击 Cut / Uncut faces（分割路径图标）。Cut face 用直线连接同一个面的边界顶点，支持外边界与孔洞之间、两个孔洞之间的连接；Uncut edge 移除相邻面之间的共享边，或移除连接不同边界的切线。已有顶点的位置和曲线控制点保持不变，每次操作都支持一步撤销和重做。

试试下面已填充的正面：选中左下角 V1，选择 Cut face → V3 并确认，新增对角线 E10 会把蓝色正面分成两个仍有填充的三角形。再次打开面板，选择 Uncut edge → E10 并确认，即可合并回来。也可以先用 Fill 清除其中一个三角形的填充；此时 Uncut 会提示两侧填充状态必须一致，避免意外改变着色范围。

切线必须位于同一个平面嵌入的面内部：穿过或接触其他边、与已有边重叠、穿过孔洞都会被拒绝。已有曲线边界和切线两侧的孔洞会保留。当前切线为直线，暂不支持任意手绘曲线。Uncut 合并两个有界面时，两侧须同时有填充或同时无填充；移除连接孔洞的切线时，保留原面的填充。悬空线段不会被作为这类切线移除。预览不会写入文档；取消、撤销、切换所选顶点或外部几何更新都会丢弃待确认的操作。操作被拒绝时会说明原因，也不会新增历史记录。

纯函数 cutVectorNetworkFace(network, from, to) 和 uncutVectorNetworkEdge(network, edgeIndex) 返回 VectorFaceTopologyResult，包含失败原因，或新网络、顶点与边的索引映射以及所选顶点。API 索引从 0 开始。填充区域会归一化为最小平面面域，保留可见着色范围和孔洞。这里的面级操作与下文已有的“在顶点处断开”Cut 工具相互独立。

连接孔洞边界

下面的环形有一个未填充的孔洞。在 Move 中选中外边界左上角 V1，打开 Cut / Uncut faces，选择 Cut face → V5。新增 E9 连接外边界和孔洞：蓝色区域仍然是一个面，孔洞保持透明，边界沿 E9 往返各一次。

再选中外边界右上角 V2，执行 Cut face → V6，新增 E10 才会把环形分成两个面。可以用 Fill 分别操作这两个面。若未改变填充，选中 V2 并 Uncut edge → E10，再选中 V1 并 Uncut edge → E9，即可恢复只有两条独立边界的环形；每步都能单独撤销和重做。

两个孔洞之间也可以这样连接，只要整条切线位于同一个面内部且不触碰其他边界。连接不同边界时减少一个边界环，面数不变；在同一边界内切分时增加一个面。已有曲线边界保持不变，填充会归一化为 evenodd 面域，保留原有的着色范围。

在顶点处断开

Cut 在选中的顶点处断开拓扑。复制该顶点，保留第一个关联端点，其余关联端点改连到副本；闭合环和开口链使用同一规则。以三角形 0—1—2—0 在顶点 1 处 Cut 为例：

plaintext

Cut 前:  0 — 1 — 2 — 0（闭合）
Cut 后:  1 — 0 — 2 — 3（3 与 1 同位置，开口折线）
segments: [0,1], [3,2], [2,0]

开口折线上则在 cut 点复制顶点，把除第一条外的 incident 边改连到副本，两条链可在 Move 模式下拖开。实现见 breakVertex：

export function breakVertex(
    network: VectorNetworkData,
    vertexIndex: number,
): VectorNetworkData | null;

Cut 模式点击顶点后调用 breakVectorNetworkAtVertex（Select.ts），写回 network、记录历史，并 setAppState({ vectorNetworkEditMode: MOVE }) 以便立刻拖拽。断开后保留仍然闭合的 regions，移除边界失效的区域；若孔洞边界失效，则移除整个所属区域，避免意外填实孔洞。清空时显式写回 regions: []，以便同步实体和撤销记录。单顶点曲线自环也支持 Cut。

课程 22 - VectorNetwork ​

SVG Path 的局限性 ​

VectorNetwork 的拓扑定义 ​

Filling ​

转换方法 ​

三角化 ​

Stroke ​

Fill ​

点击填充区域 ​

使用钢笔绘制 ​

从已有网络续画 ​

Bending ​

进入编辑态与工具条 ​

Move：线段 midpoint 插入顶点 ​

Topological operators ​

交点自动拆分 ​

Creation & delete ​

Glue & unglue ​

共享边的 Glue / Unglue ​

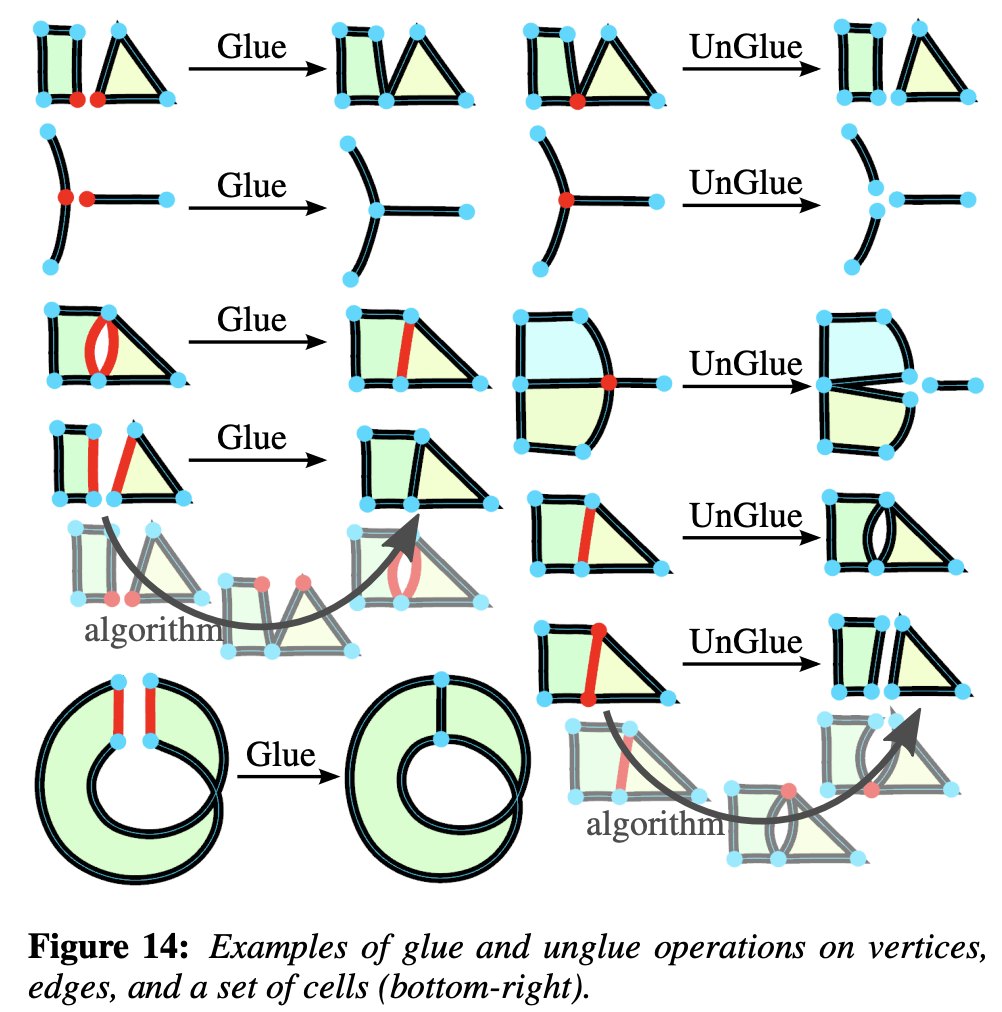
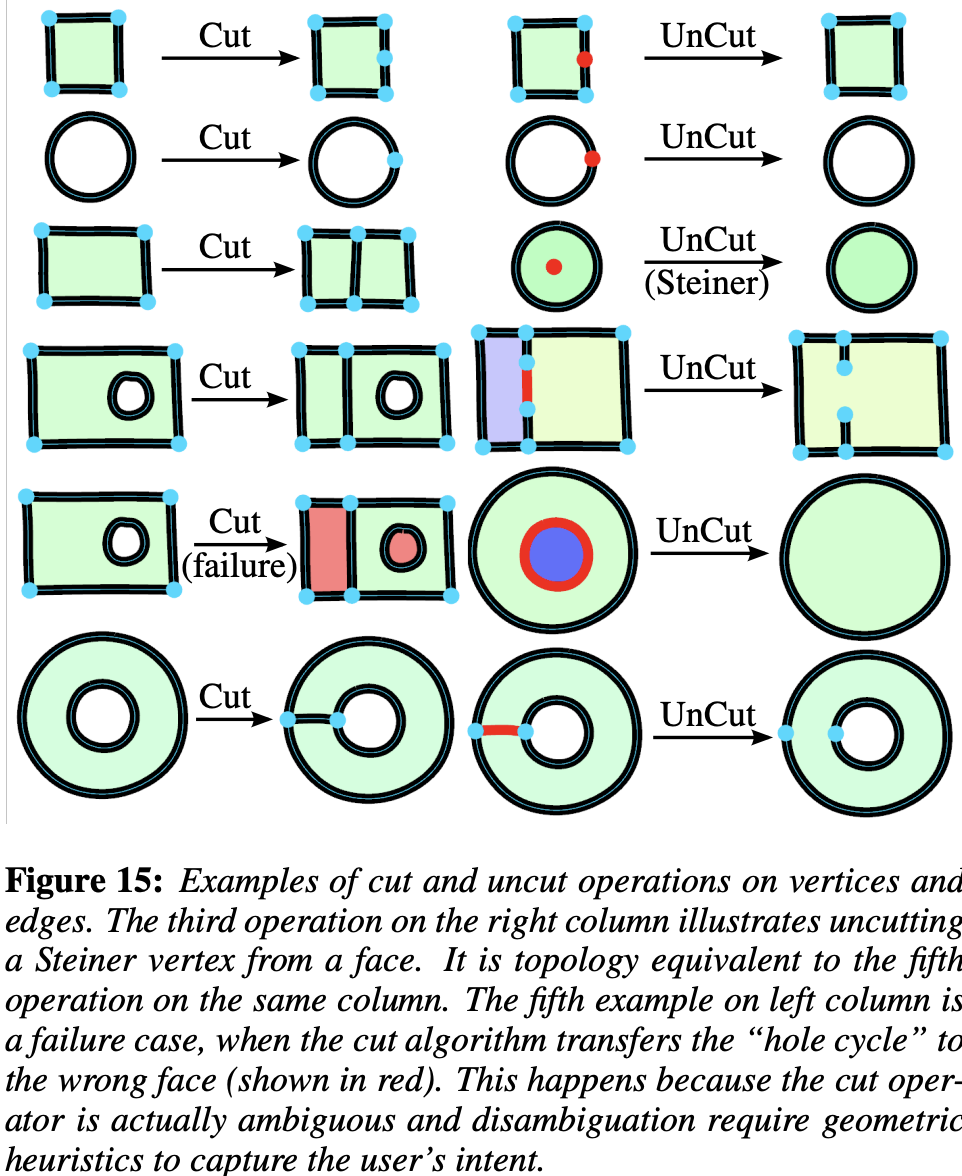
Cut & uncut ​

切分与合并面 ​

连接孔洞边界 ​

在顶点处断开 ​

扩展阅读 ​