课程 9 - 绘制椭圆和矩形

在这节课中你将学习到以下内容：

• 推导椭圆和圆角矩形的 SDF 表示
• 为包括圆角矩形在内的 SDF 增加外阴影和内阴影
• 如何判定任意点是否在椭圆或圆角矩形内

在 课程 2 中我们使用 SDF 绘制了圆形，很容易将它扩展到椭圆和矩形。2D distance functions 提供了更多 2D 图形的 SDF 表达：

float sdf_ellipse(vec2 p, vec2 r) {}
float sdf_rounded_box(vec2 p, vec2 b, vec4 r) {}

在 Shader 中使用 shape 变量区分这三种图形，这样我们就可以用同一组 Shader 绘制它们了：

if (shape < 0.5) {
  outerDistance = sdf_circle(v_FragCoord, 1.0);
  innerDistance = sdf_circle(v_FragCoord, r.x);
} else if (shape < 1.5) {
  outerDistance = sdf_ellipse(v_FragCoord, vec2(wh, 1.0));
  innerDistance = sdf_ellipse(v_FragCoord, r);
} else if (shape < 2.5) {
  outerDistance = sdf_rounded_box(v_FragCoord, vec2(wh, 1.0), 0.0);
  innerDistance = sdf_rounded_box(v_FragCoord, r, 0.0);
}

下面我们来看 SDF 是如何推导的。

矩形

The SDF of a Box 和 Leveraging Rust and the GPU to render user interfaces at 120 FPS 分别以视频和动画的形式对它的推导过程进行了展示。

基于矩形的对称性，将它的中心放置在原点后，我们可以通过 abs() 函数将任意点到矩形边缘距离的问题转换到第一象限，其中 p 为任意点坐标，b 为矩形右上角顶点坐标，由于中心和原点重合，也就是 [width / 2, height / 2]，q 表示点到右上角顶点的向量：

float sdf_box(vec2 p, vec2 b) {
  vec2 q = abs(p) - b;
}

rect SDF abs function

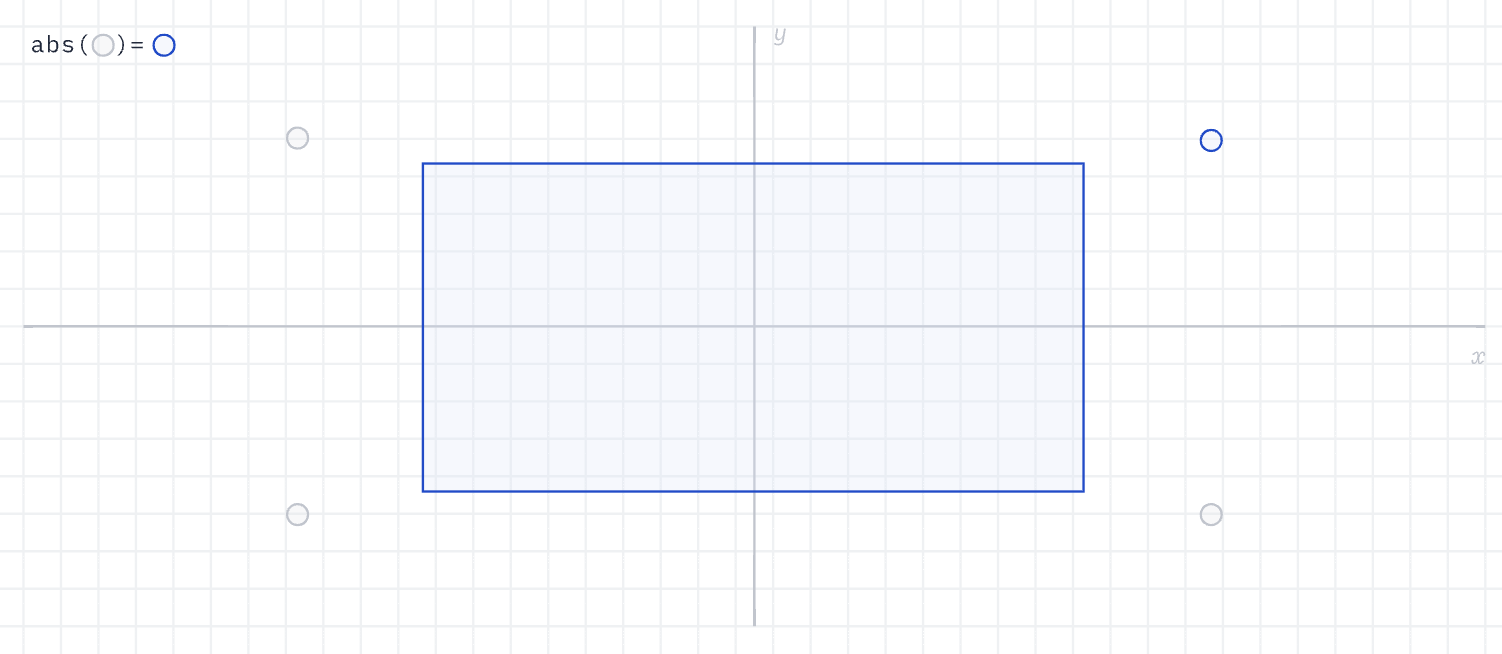
随后先考虑点在矩形外部的情况，沿着矩形右上角顶点往外延伸，又可以划分出四个象限。在下图展示的第一象限中，距离就是 q 向量的长度 length(q)，如果点落在第二象限，距离就是 q.y 因为 q.x 为负数，同理如果落在第四象限距离就是 q.x。

rect SDF

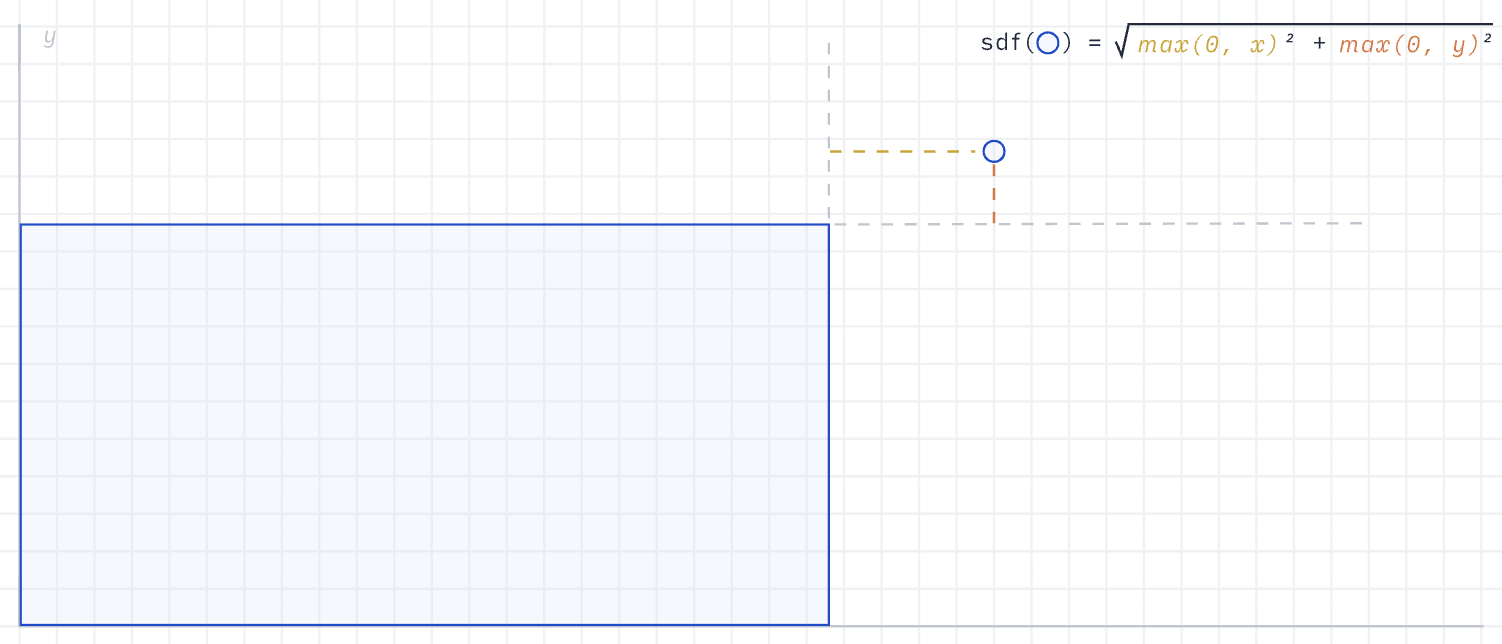
原作者很巧妙地使用 length(max(q, 0.0)) 把这三种情况统一了起来，通过 max() 消除了为负数的分量，最大程度上减少了 Shader 中的分支判断。接着再考虑点在矩形内部的情况，也就是上图中的第三象限，此时 q 的两个分量都是负数，max(q.x, q.y) 可以得到绝对值更近的距离，最外面再增加一个 min() 就可以把点在内部的情况和前三种统一起来，还是为了减少分支判断。完整 SDF 如下：

float sdf_box(vec2 p, vec2 b) {
  vec2 q = abs(p) - b;
  return length(max(q, 0.0)) + min(max(q.x, q.y), 0.0);
}

至此我们就可以绘制矩形了，参考 SVG <rect> 我们增加以下属性：

const rect = new Rect({
    x,
    y,
    width,
    height,
    fill,
});

增加圆角

下图来自 Rounding Corners in SDFs，如果我们仔细观察使用等高线可视化后的距离场，可以发现矩形本身就是圆角的。以矩形右上角附近的点为例，距离相等的点不止一个，它们刚好分布在以右上角顶点为圆心的圆上。

rounded rect sdf

事实上不仅是矩形，所有使用 SDF 表示的图形都可以转换成“圆角”版本，下图来自 2D distance functions：

float opRound( in vec2 p, in float r ) {
  return sdShape(p) - r;
}

more rounded shapes

因此完整的圆角矩形 SDF 表示如下：

float sdf_rounded_box(vec2 p, vec2 b, float r) {
  vec2 q = abs(p) - b + r;
  return length(max(q, 0.0)) + min(max(q.x, q.y), 0.0) - r;
}

参考 Figma 的命名我们使用 cornerRadius，但仅凭 SDF 无法实现 smoothing 效果，详见 Adjust corner radius and smoothing 和 Desperately seeking squircles。另外也可以支持四个角不同的圆角半径，可以参考 Zed Blade WGSL，这是 Zed 基于 blade 渲染器编写的 Shader，使用 WGSL 语法。

$icCanvas2 = call(() => {
    return document.createElement('ic-canvas-lesson9');
});

call(() => {
    const { Canvas, Rect } = Lesson9;

    const stats = new Stats();
    stats.showPanel(0);
    const $stats = stats.dom;
    $stats.style.position = 'absolute';
    $stats.style.left = '0px';
    $stats.style.top = '0px';

    $icCanvas2.parentElement.style.position = 'relative';
    $icCanvas2.parentElement.appendChild($stats);

    $icCanvas2.addEventListener('ic-ready', (e) => {
        const canvas = e.detail;

        for (let i = 0; i < 1000; i++) {
            const fill = `rgb(${Math.floor(Math.random() * 255)},${Math.floor(
                Math.random() * 255,
            )},${Math.floor(Math.random() * 255)})`;
            const rect = new Rect({
                x: Math.random() * 1000,
                y: Math.random() * 1000,
                fill,
                cornerRadius: 10,
            });
            // rect.x = Math.random() * 1000;
            // rect.y = Math.random() * 1000;
            rect.width = Math.random() * 40;
            rect.height = Math.random() * 40;
            canvas.appendChild(rect);

            rect.addEventListener('pointerenter', () => {
                rect.fill = 'red';
            });
            rect.addEventListener('pointerleave', () => {
                rect.fill = fill;
            });
        }
    });

    $icCanvas2.addEventListener('ic-frame', (e) => {
        stats.update();
    });
});

增加外阴影

提起阴影，你可能听说过 CSS 中的 box-shadow 和 filter: drop-shadow()。下图来自 Drop-Shadow: The Underrated CSS Filter 一文，直观展示了两者的区别：

Compare box-shadow with drop-shadow

通常后者更常用，例如 tailwindcss - Drop Shadow。因此我们为矩形增加如下属性：

rect.dropShadowColor = 'black';
rect.dropShadowOffsetX = 10;
rect.dropShadowOffsetY = 10;
rect.dropShadowBlurRadius = 5;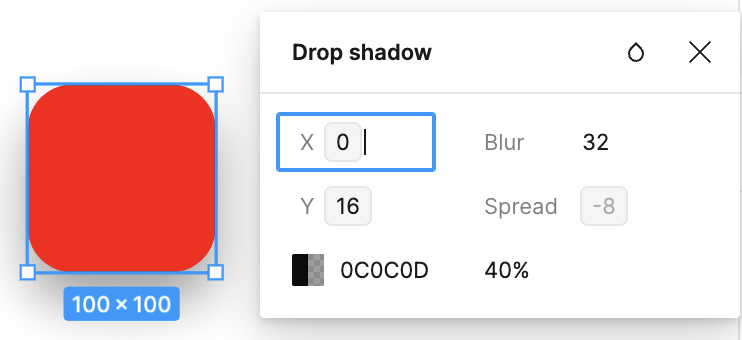

Drop shadow in Figma

接下来我们着手使用 WebGL / WebGPU 为 2D 图形绘制阴影。通常会使用后处理中的高斯模糊，例如 Pixi.js 的 DropShadowFilter。2D 高斯模糊效果可以分解成水平和垂直两次 1D 效果从而独立进行，但卷积操作还是需要对相邻像素点（取决于卷积核的大小）进行采样。

Figma 的 CTO Evan Wallace 在 Fast Rounded Rectangle Shadows 一文中介绍了一种更快速的近似方法，无需对纹理进行采样，Leveraging Rust and the GPU to render user interfaces at 120 FPS 一文也对该方法进行了更详细的介绍。高斯函数与阶跃函数的卷积等同于高斯函数的积分，其结果为误差函数 Error function（也称为 erf）。因此生成一个模糊的矩形相当于分别模糊每个维度，然后取两个结果的交集，这里先不考虑圆角情况。

高斯函数为：

$$f(x)=\frac{\exp (-x^2/(2{\sigma }^2))}{(\sigma \sqrt{2\pi })}$$

误差函数是高斯函数的积分，用于描述正态分布的累积分布函数。

$$\int f(x)dx=F(x)$$$$F(x)=\frac{(1+erf(\frac{x}{\sigma \sqrt{2}}))}{2}$$

误差函数的一个常用近似来自 Abramowitz and Stegun. Handbook of Mathematical Functions.：

$$erf(x)\approx \frac{x}{1+a{x}^2+b{x}^4+c{x}^6+d{x}^8+e{x}^{10}}$$

其中多项式各项系数为：

$$\begin{array}{c}a=0.278393,\\ b=0.230389,\\ c=0.000972,\\ d=0.078108,\\ e=2.03380\times {10}^{-4}\end{array}$$

下面的实现来自 Zed Blade WGSL，我们将其用 GLSL 简单改写下。Blurred rounded rectangles 提供了另一个版本的 erf 实现：

vec2 erf(vec2 x) {
  vec2 s = sign(x), a = abs(x);
  x = 1.0 + (0.278393 + (0.230389 + 0.078108 * (a * a)) * a) * a;
  x *= x;
  return s - s / (x * x);
}

先不考虑圆角，计算最终的阴影遮罩值。这里通过 integral_x 和 integral_y 的差值来确定阴影的边界。integral_x.x - integral_x.y 计算了 x 轴上阴影的宽度，integral_y.x - integral_y.y 计算了 y 轴上阴影的高度。将这两个值相乘得到最终的阴影遮罩值。

// Return the mask for the shadow of a box from lower to upper
float rect_shadow(vec2 pixel_position, vec2 origin, vec2 size, float sigma) {
  vec2 bottom_right = origin + size;
  vec2 x_distance = vec2(pixel_position.x - origin.x, pixel_position.x - bottom_right.x);
  vec2 y_distance = vec2(pixel_position.y - origin.y, pixel_position.y - bottom_right.y);
  vec2 integral_x = 0.5 + 0.5 * erf(x_distance * (sqrt(0.5) / sigma));
  vec2 integral_y = 0.5 + 0.5 * erf(y_distance * (sqrt(0.5) / sigma));
  return (integral_x.x - integral_x.y) * (integral_y.x - integral_y.y);
}

然而，对于圆角矩形与高斯函数的二维卷积，并不存在着像上述那样的封闭形式的解，因为圆角矩形的公式不可分离。Evan Wallace 的近似方法的巧妙之处在于，沿着一个轴进行封闭形式的精确卷积，然后手动将高斯函数沿着相反轴滑动有限次：

float blur_along_x(float x, float y, float sigma, float corner, vec2 half_size) {
  float delta = min(half_size.y - corner - abs(y), 0.);
  float curved =
  half_size.x - corner + sqrt(max(0., corner * corner - delta * delta));
  vec2 integral =
  0.5 + 0.5 * erf((x + vec2(-curved, curved)) * (sqrt(0.5) / sigma));
  return integral.y - integral.x;
}

// The signal is only non-zero in a limited range, so don't waste samples
float low = center_to_point.y - half_size.y;
float high = center_to_point.y + half_size.y;
float start = clamp(-3. * blur_radius, low, high);
float end = clamp(3. * blur_radius, low, high);

// Accumulate samples (we can get away with surprisingly few samples)
float step = (end - start) / 4.;
float y = start + step * 0.5;

for (int i = 0; i < 4; i++) {
  alpha += blur_along_x(center_to_point.x, center_to_point.y - y, blur_radius,
                        cornerRadius, half_size) *
          gaussian(y, blur_radius) * step;
  y += step;
}

在实现中，对于每个矩形都需要单独绘制阴影，这会打破之前合批的效果。原因是我们必须严格按照绘制次序执行，甚至每次重绘前都需要重新排序。下面的代码来自 Fast Rounded Rectangle Shadows，在绘制之前需要按预先设置的深度为所有矩形排序，然后依次绘制阴影和本体：

render() {
  boxes.sort(function(a, b) {
    return a.depth - b.depth;
  });
  for (var i = 0; i < boxes.length; i++) {
    boxes[i].callback(); // 先后绘制阴影和矩形
  }
}

以下面的两个矩形为例，绘制次序为：绿色矩形的阴影，绿色矩形，红色矩形阴影，红色矩形。如果按照之前的思路，把两个阴影和两个矩形本体分别合并成两批绘制，就无法让红色矩形的阴影投射在绿色矩形上。因此在使用时，我们需要为带阴影的矩形设置 batchable = false

$icCanvas3 = call(() => {
    return document.createElement('ic-canvas-lesson9');
});

call(() => {
    const { Canvas, Rect } = Lesson9;

    const stats = new Stats();
    stats.showPanel(0);
    const $stats = stats.dom;
    $stats.style.position = 'absolute';
    $stats.style.left = '0px';
    $stats.style.top = '0px';

    $icCanvas3.parentElement.style.position = 'relative';
    $icCanvas3.parentElement.appendChild($stats);

    $icCanvas3.addEventListener('ic-ready', (e) => {
        const canvas = e.detail;

        const rect = new Rect({
            x: 50,
            y: 50,
            fill: 'green',
            cornerRadius: 50,
            batchable: false,
            dropShadowColor: 'black',
            dropShadowOffsetX: 10,
            dropShadowOffsetY: 10,
            dropShadowBlurRadius: 10,
        });
        rect.width = 400;
        rect.height = 100;
        canvas.appendChild(rect);

        const rect2 = new Rect({
            x: 100,
            y: 100,
            fill: 'red',
            batchable: false,
            cornerRadius: 50,
            dropShadowColor: 'black',
            dropShadowBlurRadius: 10,
        });
        rect2.width = 400;
        rect2.height = 100;
        canvas.appendChild(rect2);
    });

    $icCanvas3.addEventListener('ic-frame', (e) => {
        stats.update();
    });
});

还有一点需要注意，由于阴影模糊半径的存在，需要让矩形在原有尺寸上外扩一圈，这里设置为 3 * dropShadowBlurRadius

float margin = 3.0 * dropShadow.z;
origin += dropShadow.xy;
v_Origin = origin; // 原始顶点
v_Size = size; // 原始尺寸

origin -= margin;
size += 2.0 * margin;
vec2 center = origin + size / 2.0;
v_Point = center + a_FragCoord * (size / 2.0);

最后阴影也会影响 RenderBounds 的计算，否则当矩形主体在视口之外，但阴影在视口之内时会被错误地剔除：

this.renderBounds.addBounds(
    new AABB(
        x + dropShadowOffsetX - dropShadowBlurRadius,
        y + dropShadowOffsetY - dropShadowBlurRadius,
        x + dropShadowOffsetX + width + dropShadowBlurRadius,
        y + dropShadowOffsetY + height + dropShadowBlurRadius,
    ),
);

基于这种方法，还可以实现一些有趣的效果，详见：Shape Lens Blur Effect with SDFs and WebGL

但显然上面的方法只适用于圆角矩形，是否有针对圆、椭圆以及其他 SDF 表示更通用的方法呢？Shader toy 上有一个例子：Drop shadow of rounded rect，有趣的是，根据这个例子衍生的另一个示例可以进行外阴影和内阴影的实现。下面我们着重介绍内阴影的实现。

增加内阴影

下图为 Figma 的内阴影效果，常用于 Button 这样的 UI 组件。

Inner shadow in Figma

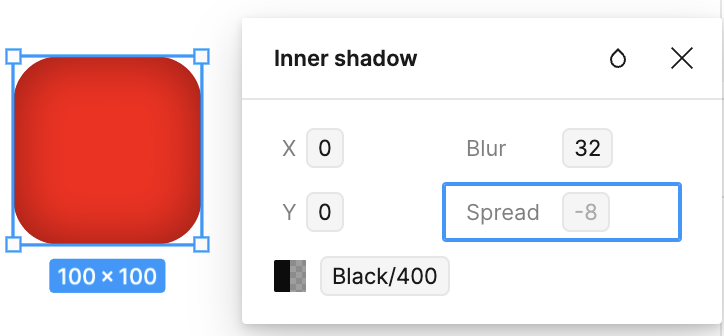
让我们增加如下属性：

rect.innerShadowColor = 'black';
rect.innerShadowOffsetX = 10;
rect.innerShadowOffsetY = 10;
rect.innerShadowBlurRadius = 5;

参考 Shader toy 上的例子：Inner shadow of rounded rect 我们同样为目前的三个图形分别增加阴影绘制逻辑，使用 sigmoid 将输入值在 [0, 1] 间进行平滑处理：

float make_shadow(vec2 pos, vec2 halfSize, float cornerRd, float blurRd, float distMul, float shape) {
  float distance;
  if (shape < 0.5) {
    distance = sdf_circle(pos, halfSize.x);
  } else if (shape < 1.5) {
    distance = sdf_ellipse(pos, halfSize);
  } else if (shape < 2.5) {
    distance = sdf_rounded_box(pos, halfSize, cornerRd + blurRd);
  }
  float dist = sigmoid(distMul * distance / blurRd);
  return clamp(dist, 0.0, 1.0);
}

$icCanvas4 = call(() => {
    return document.createElement('ic-canvas-lesson9');
});

call(() => {
    const { Canvas, Rect, Circle, Ellipse } = Lesson9;

    const stats = new Stats();
    stats.showPanel(0);
    const $stats = stats.dom;
    $stats.style.position = 'absolute';
    $stats.style.left = '0px';
    $stats.style.top = '0px';

    $icCanvas4.parentElement.style.position = 'relative';
    $icCanvas4.parentElement.appendChild($stats);

    $icCanvas4.addEventListener('ic-ready', (e) => {
        const canvas = e.detail;
        for (let i = 0; i < 10; i++) {
            const fill = `rgb(${Math.floor(Math.random() * 255)},${Math.floor(
                Math.random() * 255,
            )},${Math.floor(Math.random() * 255)})`;

            const rect = new Rect({
                x: Math.random() * 1000,
                y: Math.random() * 1000,
                fill,
                cornerRadius: 50,
                innerShadowColor: 'black',
                innerShadowOffsetX: Math.random() * 20 - 10,
                innerShadowOffsetY: Math.random() * 20 - 10,
                innerShadowBlurRadius: Math.random() * 10,
            });
            rect.width = 200;
            rect.height = 100;
            canvas.appendChild(rect);

            const circle = new Circle({
                cx: Math.random() * 1000,
                cy: Math.random() * 1000,
                r: 100,
                fill,
                innerShadowColor: 'black',
                innerShadowOffsetX: Math.random() * 20 - 10,
                innerShadowOffsetY: Math.random() * 20 - 10,
                innerShadowBlurRadius: Math.random() * 10,
            });
            canvas.appendChild(circle);

            const ellipse = new Ellipse({
                cx: Math.random() * 1000,
                cy: Math.random() * 1000,
                rx: 100,
                ry: 50,
                fill,
                innerShadowColor: 'blue',
                innerShadowOffsetX: Math.random() * 20 - 10,
                innerShadowOffsetY: Math.random() * 20 - 10,
                innerShadowBlurRadius: Math.random() * 10,
            });
            canvas.appendChild(ellipse);
        }
    });

    $icCanvas4.addEventListener('ic-frame', (e) => {
        stats.update();
    });
});

椭圆

不同于判断任意点到圆上的最近距离，针对椭圆的精确分析方法要复杂得多，Distance to an ellipse 给出了两种方法：一元四次方程和 Newton 方法。

求解一元四次方程

椭圆使用 $q(\omega )=\{a\cdot cos\omega ,b\cdot sin\omega \}$ 表示，任意点 $p$ 到椭圆上点的距离平方为：

$$s^2(\omega )={|q(\omega )-p|}^2$$

展开后：

$$a^{2}co{s}^2\omega +b^{2}si{n}^2\omega +x^2+y^2-2(axcos\omega -bysin\omega )$$

对 $\omega$ 求导得到：

$$-2a^{2}sin\omega \cdot cos\omega +2b^{2}cos\omega \cdot sin\omega +2axsin\omega -2bycos\omega$$

最近点导数为 0，将 $\lambda =cos\omega$ 带入得到：

$$\sqrt{1-{\lambda }^2}((b^2-a^2)\lambda +ax)=by\lambda$$

这是一个关于 $\lambda$ 的一元四次方程，各项系数为：

$$\begin{array}{c}{a}_4={(b^2-a^2)}^2\\ a_3=2ax(b^2-a^2)\\ a_2=(a^2{x}^2+b^2{y}^2)-{(b^2-a^2)}^2\\ a_1=-2ax(b^2-a^2)\\ a_0=-a^2{x}^2\end{array}$$

为了将四次项的系数化成 1 得到 Monic Polynomial，将上述每个系数都除以 $a_4$，而且是椭圆的缘故不用担心除以 0 的问题。同时使用 $mn$ 代入：

$$m=x\frac{a}{b^2-a^2}n=y\frac{b}{b^2-a^2}$$

这样就得到了 Quartic Equation，各项系数如下：

$$\begin{array}{c}{a}_4=1\\ a_3=2m\\ a_2=m^2+n^2-1\\ a_1=-2m\\ a_0=-m^2\end{array}$$

由于最高次系数为 1，可以使用 Resolvent Cubic，转化为对一元三次方程 Cubic Formula 的求解问题：

$$\begin{array}{c}f(x)=x^4+a_3{x}^3+a_2{x}^2+a_{1}x+a_0\\ g(x)=x^3+b_2{x}^2+b_{1}x+b_0\end{array}$$

其中系数的对应关系为：

$$b_2=-a_2{b}_1=a_1{a}_3-4a_0{b}_0=4a_0{a}_2-a_1^2-a_0{a}_3^2$$

代入后：

$$b_2=-(m^2+n^2-1)b_1=0b_0=-4m^2{n}^2$$

解 Cubic Formula 需要尝试消除二项式系数，令 $z=x-1/3k_2$ 可以做到。此时得到标准形式为：$x^3+px=q$ 其中：

$$p=(3k_1-k_2^2)/3q=(9k_1{k}_2-27k_0-2k_2^3)/27$$

代入$b_0{b}_1{b}_2$可得：

$$\begin{array}{c}p=-(m^2+n^2-1{)}^2/3\\ q=4m^2{n}^2+2(m^2+n^2-1{)}^3/27\end{array}$$

继续简化上式，令：

$$\begin{array}{c}Q=(\frac{m^2+n^2-1}{3}{)}^2\\ R=2m^2{n}^2+(\frac{m^2+n^2-1}{3}{)}^3\end{array}$$

标准形式变成：$x^3-3Qx+2R=0$

这种方法计算开销很大，Distance to an ellipse 中展示了在 ShaderToy 上编写的例子，和下面要介绍的两种方法相比 FPS 会低很多。

牛顿法

任意点 $p$ 到椭圆上距离最近点 $q$ 形成的向量一定是垂直于椭圆在 $q$ 点的切线的。

$$<p-q(\omega ),q^{\prime }(\omega )>=0$$

其中：

$$q^{\prime }(\omega )=(-a\cdot sin\omega ,b\cdot cos\omega )$$

代入后得到：

$$\begin{array}{c}f(\omega )=-a\cdot sin\omega \cdot (x-a\cdot cos\omega )+b\cdot cos\omega \cdot (y-b\cdot sin\omega )=0\\ f^{\prime }(\omega )=-<p-u,v>-<v,v>\\ u=(a\cdot cos\omega ,b\cdot sin\omega )\\ v=(-a\cdot sin\omega ,b\cdot cos\omega )\end{array}$$

Newton's method，它是一种在实数域和复数域上近似求解方程的方法。

$$x_{n+1}=x_n-\frac{f(x_n)}{f^{\prime }(x_n)}$$

代入后得到：

$${\omega }_{n+1}={\omega }_n+\frac{<p-u,v>}{<p-u,u>+<v,v>}$$

Distance to an ellipse 原作者使用了 5 次迭代就可以达到非常好的效果：

for (int i=0; i<5; i++) {
  vec2 cs = vec2(cos(w),sin(w));
  vec2 u = ab*vec2( cs.x,cs.y);
  vec2 v = ab*vec2(-cs.y,cs.x);
  w = w + dot(p-u,v)/(dot(p-u,u)+dot(v,v));
}

下面只需要找到 ${\omega }_0$。还是利用对称性，只考虑点在第一象限的情况，首先判断点是否在椭圆内，代入椭圆方程即可：

bool s = dot(p/ab,p/ab)>1.0;

如果在椭圆外，可以先拉伸成圆（下面一小节介绍的方法也会用到），此时 ${\omega }_0=atan(y/x)$，再反向拉伸回椭圆： ${\omega }_0=atan(a\cdot y/b\cdot x)$

如果在椭圆内，选择半长轴 $0$ 或短轴 $\pi /2$ 作为起点：

float w = s ? atan(p.y*ab.x, p.x*ab.y) :
  ((ab.x*(p.x-ab.x)<ab.y*(p.y-ab.y))? 1.5707963 : 0.0);

相比之前解一元四次方程，这种方法的开销要小一些。但毕竟还是包含一个固定迭代次数的 for 循环，在编译 GLSL 时会将循环展开，可参考：Loop performance in a shader。 最后我们会介绍一种近似估计的方法，开销是最小的。

拉伸成圆近似法

Ellipsoid SDF 介绍了这种方法，先拉伸成单位圆，再恢复成椭圆。但在恢复时如何选择拉伸系数呢？如果点在 X 轴上，系数就是 r.x，在 Y 轴上是 r.y，首先选择两者的较小值：

float sdf_ellipse_V1( in vec2 p, in vec2 r )
{
  float k1 = length(p/r);
  return (k1-1.0)*min(r.x,r.y);
}

实际渲染后发现这种方式在长轴处存在明显的问题，并不贴合：

artifact on ellipse's edge

原作者给出了改进版：

float sdf_ellipse_V3( in vec3 p, in vec3 r )
{
  float k1 = length(p/r);
  return length(p)*(1.0-1.0/k1);
}

但实际渲染后发现这种方式在边缘处存在明显的锯齿：

artifact on ellipse's edge

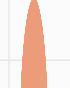
最终作者加入了对梯度的考虑，我们也使用这种方式：

float sdf_ellipse_V2( in vec2 p, in vec2 r )
{
  float k1 = length(p/r);
  float k2 = length(p/(r*r));
  return k1*(k1-1.0)/k2;
}

可以看到效果好了很多，在一些极端情况贴合的也很紧实。

$icCanvas = call(() => {
    return document.createElement('ic-canvas-lesson9');
});

call(() => {
    const { Canvas, Ellipse } = Lesson9;

    const stats = new Stats();
    stats.showPanel(0);
    const $stats = stats.dom;
    $stats.style.position = 'absolute';
    $stats.style.left = '0px';
    $stats.style.top = '0px';

    $icCanvas.parentElement.style.position = 'relative';
    $icCanvas.parentElement.appendChild($stats);

    $icCanvas.addEventListener('ic-ready', (e) => {
        const canvas = e.detail;

        for (let i = 0; i < 1000; i++) {
            const fill = `rgb(${Math.floor(Math.random() * 255)},${Math.floor(
                Math.random() * 255,
            )},${Math.floor(Math.random() * 255)})`;
            const ellipse = new Ellipse({
                cx: Math.random() * 1000,
                cy: Math.random() * 1000,
                rx: Math.random() * 20,
                ry: Math.random() * 20,
                fill,
            });
            canvas.appendChild(ellipse);
            ellipse.addEventListener('pointerenter', () => {
                ellipse.fill = 'red';
            });
            ellipse.addEventListener('pointerleave', () => {
                ellipse.fill = fill;
            });
        }
    });

    $icCanvas.addEventListener('ic-frame', (e) => {
        stats.update();
    });
});

拾取判定

目前我们的拾取插件使用数学方法，因此需要为椭圆和圆角矩形分别实现判定方法，后续我们会介绍更为通用的基于颜色编码的 GPU 拾取方式。在上面的两个示例中，你可以将鼠标悬停到任意图形上体验拾取效果。

椭圆

椭圆的拾取判定比较简单，例如默认情况下填充和描边区域都要考虑：

function isPointInEllipse(
    x: number,
    y: number,
    h: number,
    k: number,
    a: number,
    b: number,
) {
    // 计算点到椭圆中心的 x 和 y 坐标差
    const dx = x - h;
    const dy = y - k;

    // 计算点相对于椭圆中心的坐标平方，然后除以半轴长度的平方
    const squaredDistance = (dx * dx) / (a * a) + (dy * dy) / (b * b);

    // 如果计算结果小于或等于 1，则点在椭圆内
    return squaredDistance <= 1;
}

圆角矩形

如果不考虑圆角，矩形的判定也非常简单。

function isPointInRoundedRectangle(
    x: number,
    y: number,
    x1: number,
    y1: number,
    x2: number,
    y2: number,
    r: number,
) {
    // 判断点是否在矩形的四个角的圆角内
    function isInsideCorner(
        x: number,
        y: number,
        cornerX: number,
        cornerY: number,
        r: number,
    ) {
        const distance = Math.sqrt(
            Math.pow(x - cornerX, 2) + Math.pow(y - cornerY, 2),
        );
        return distance <= r;
    }

    // 判断点是否在圆角矩形内
    if (x >= x1 && x <= x2 && y >= y1 && y <= y2) {
        // 点在矩形内部
        if (
            isInsideCorner(x, y, x1 + r, y1 + r, r) || // 左上角
            isInsideCorner(x, y, x2 - r, y1 + r, r) || // 右上角
            isInsideCorner(x, y, x2 - r, y2 - r, r) || // 右下角
            isInsideCorner(x, y, x1 + r, y2 - r, r) // 左下角
        ) {
            return true; // 点在圆角内
        }
        return !(
            x <= x1 + r ||
            x >= x2 - r || // 点在矩形的非圆角边界上
            y <= y1 + r ||
            y >= y2 - r
        );
    }
    return false; // 点不在矩形内
}

扩展阅读

• Distance to an ellipse
• Distance from a Point to an Ellipse, an Ellipsoid, or a Hyperellipsoid
• Fast Rounded Rectangle Shadows
• Blurred rounded rectangles
• Desperately seeking squircles