Lesson 22 - VectorNetwork
In this lesson, you will learn about:
- Limitations of SVG Path
- What is VectorNetwork?
- Using the Pen tool to modify Path
Limitations of SVG Path
In Lesson 13, we learned about Path drawing. Figma also provides the VectorPath API, which supports a subset of SVG Path commands (see: VectorPath-data) and fillRule (called windingRule in Figma).
node.vectorPaths = [
{
windingRule: 'EVENODD',
data: 'M 0 100 L 100 100 L 50 0 Z',
},
];So why introduce the VectorNetwork API? The reason is that SVG Path has some inherent limitations. The Engineering behind Figma's Vector Networks article vividly demonstrates this. The following shape cannot be described using just one Path:

It can only be described by splitting into multiple Paths. While this is possible, certain intuitive operations cannot be achieved in editing scenarios. For example, when dragging the center vertex at the bottom left, only one vertex will follow because it consists of two independent Paths:

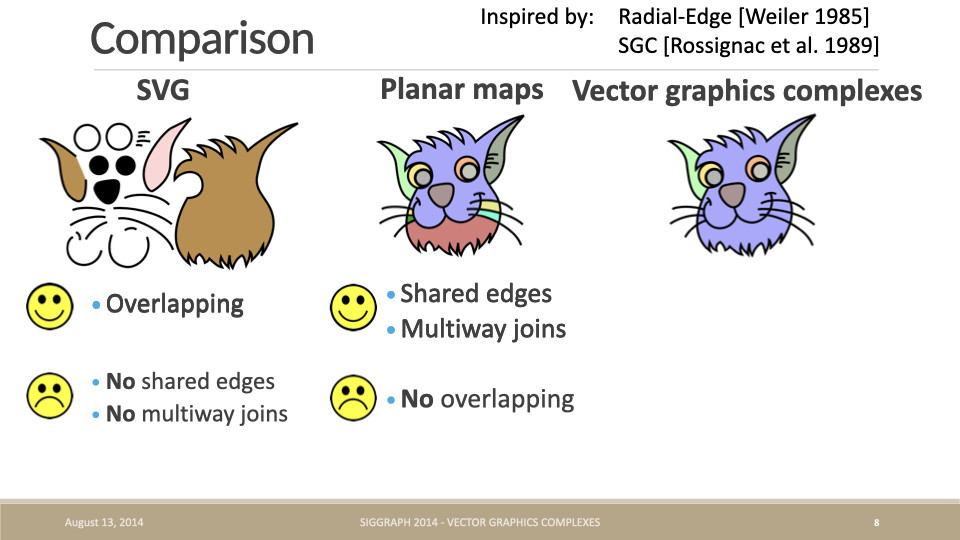
Besides vertices not being able to have more than 2 edges, edges cannot be shared either. The original paper and PPT of Vector Graphics Complexes compare SVG and Planar maps, neither of which can support overlapping, shared vertices, and edges, leading to a new geometric representation (hereinafter referred to as VGC):
vpaint is implemented based on VGC. You can see how natural the interactive effects are during editing after merging points and edges:
Or using the example of dragging an edge of a cube from The Engineering behind Figma's Vector Networks:

It's worth mentioning that the Discussion in HN points out the remarkable similarity between VGC and Figma's VectorNetwork. Considering that both started exploring around the same time, they arrived at similar solutions through different paths, hence we'll use the term VectorNetwork in the following text.
CEO of Figma here. Most of the original insights around vector networks were in 2013, though we continued to polish the implementation over time. We didn't exit stealth and ship the closed beta of Figma until December 2015 which is why there isn't blog content before then. At first glance, this thesis looks super neat! I'm excited to check it out! I don't believe I've seen it before which is surprising given the overlap.
Let's look at how VectorNetwork is defined.
Topology Definition of VectorNetwork
The definition of VectorNetwork/VGC is much more complex than Path. Its data structure is a graph consisting of vertices, edges, and faces (filled regions). The following image is from the original Vector Graphics Complexes paper.
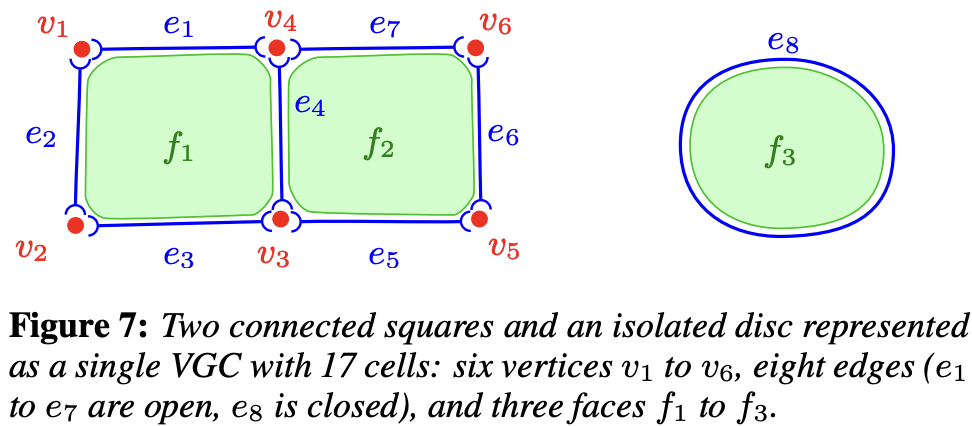
Here we only discuss the topology definition. Other drawing attributes can remain consistent with Path:
On top of this core structure, more drawing attributes can be added for fine control on rendering. For instance, we added vertex radius, variable edge width, cell color (possibly transparent), and edge junctions style (mitre join or bevel join).
Vertices are easy to understand. In VGC, edges consist of a pair of start and end vertex indices, forming a self-loop when they coincide.
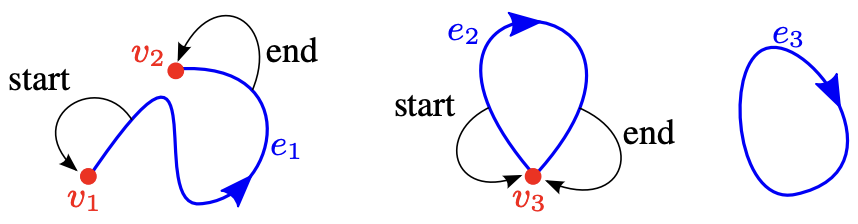
Filled regions are defined by closed loops of vertices. In VGC, they are defined using a set of halfedges:
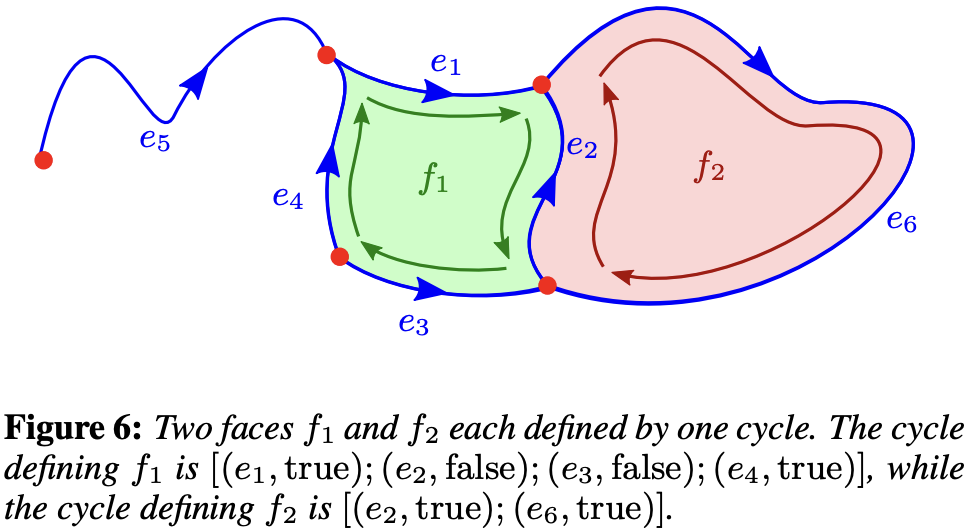
The following triangle example is from the VectorNetwork API. You can see it's basically consistent with VGC, except that filled regions are defined by vertex indices and fillRule. Other non-geometric attributes like strokeCap remain consistent with Path:
node.vectorNetwork = {
// The vertices of the triangle
vertices: [
{ x: 0, y: 100 },
{ x: 100, y: 100 },
{ x: 50, y: 0 },
],
// The edges of the triangle. 'start' and 'end' refer to indices in the vertices array.
segments: [
{
start: 0,
tangentStart: { x: 0, y: 0 }, // optional
end: 1,
tangentEnd: { x: 0, y: 0 }, // optional
},
{
start: 1,
end: 2,
},
{
start: 2,
end: 0,
},
],
// The loop that forms the triangle. Each loop is a
// sequence of indices into the segments array.
regions: [{ windingRule: 'NONZERO', loops: [[0, 1, 2]] }],
};In editing scenarios, vertices and edges are defined by users, while filled regions need to be automatically calculated by the system. So how do we find these filled regions?
Filling
In operations like click to fill, we need to find the minimum loop formed by vertices.
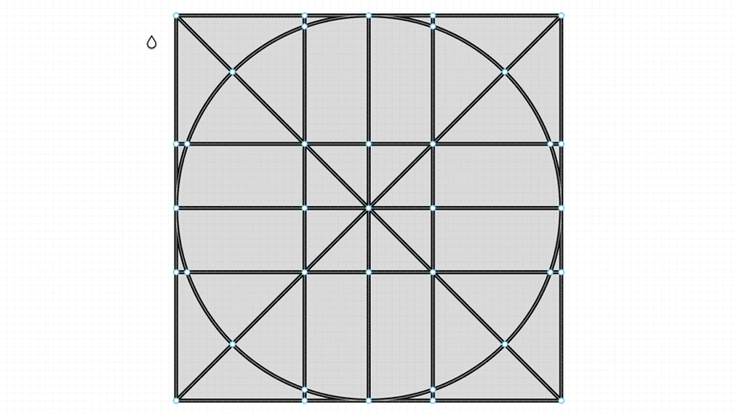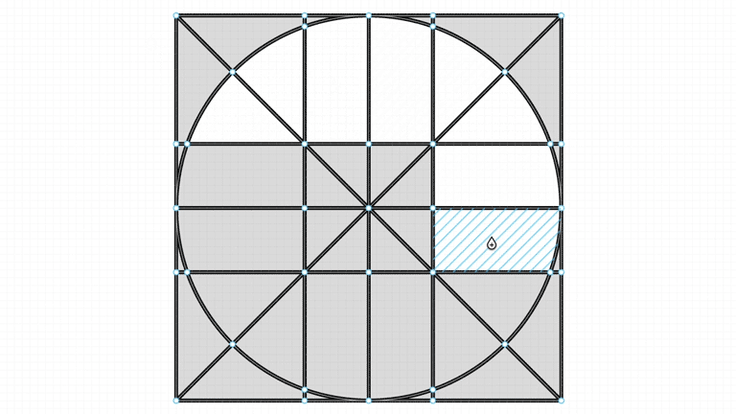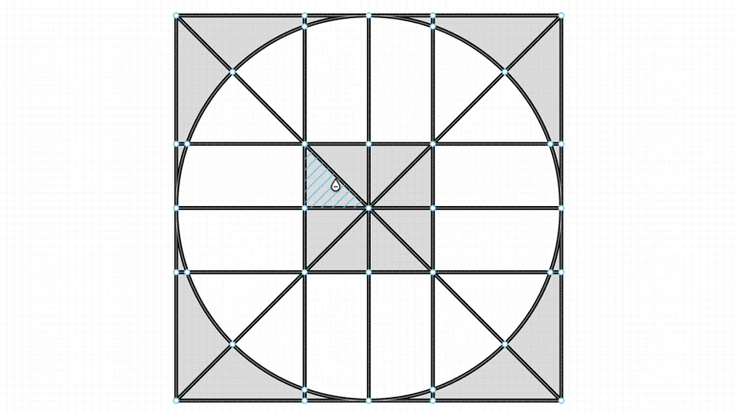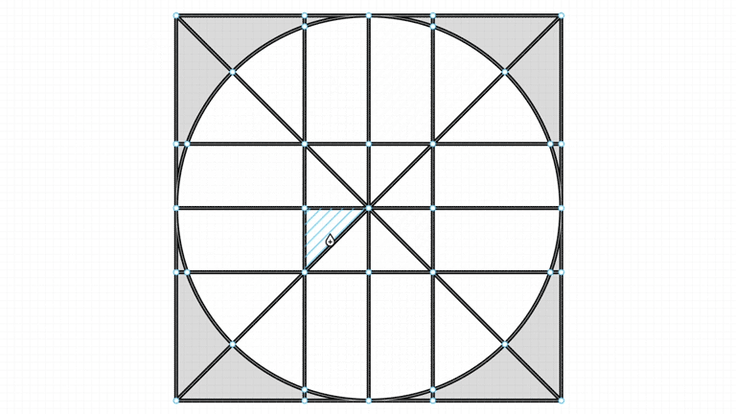
Bending
The following is from Introducing Vector Networks - Bending. For Bezier curve editing, it's common in both Path and VectorNetwork:
Vector graphics today are based on cubic bezier splines, which are curves with two extra points called control handles that are positioned away from the curve itself and that control how much it bends, sort of like how a magnet might bend a wire towards it. Changing the shape of a curve involves dragging a control handle off in space instead of dragging the curve directly.

In VectorNetwork's edge definition, tangentStart and tangentEnd can define the two control points of a cubic Bezier curve. When both are [0, 0], it degenerates into a straight line.
Topological operators
Creation & delete
Delete and Heal for Vector Networks
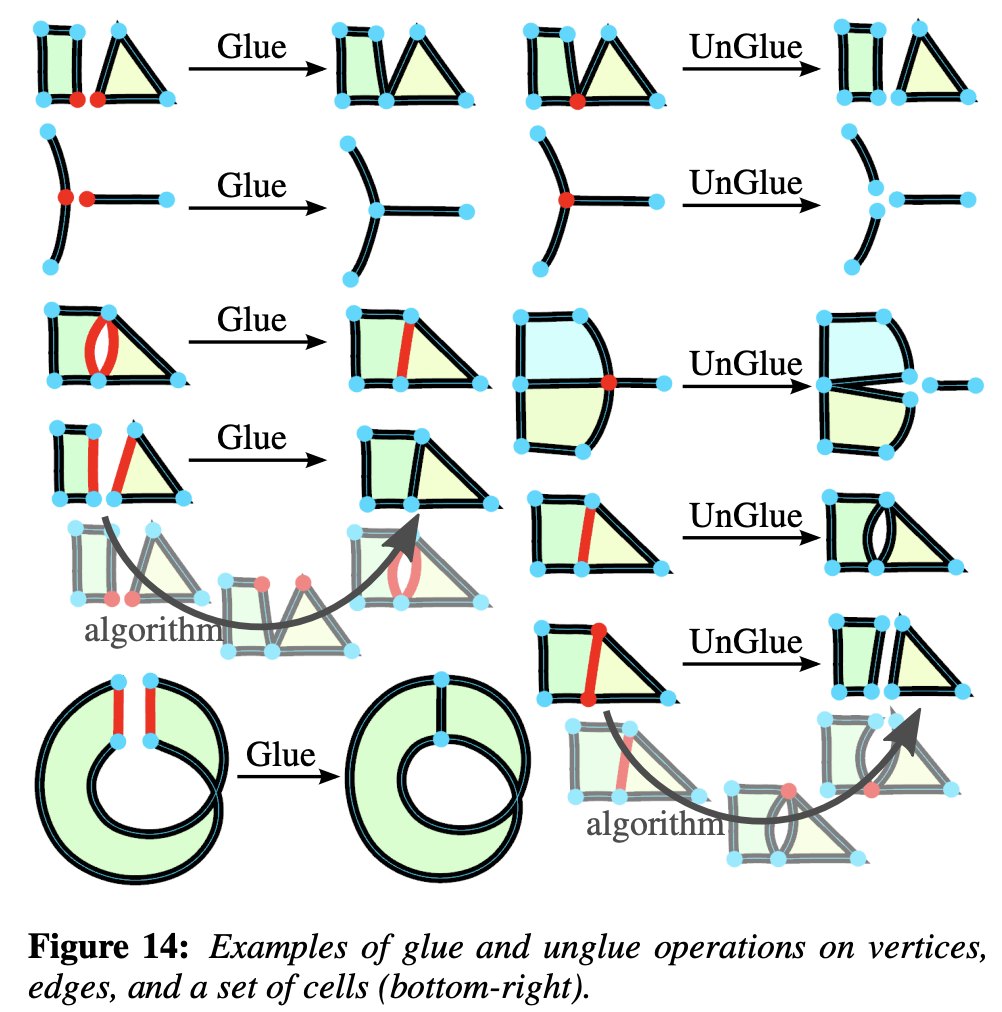
Glue & unglue
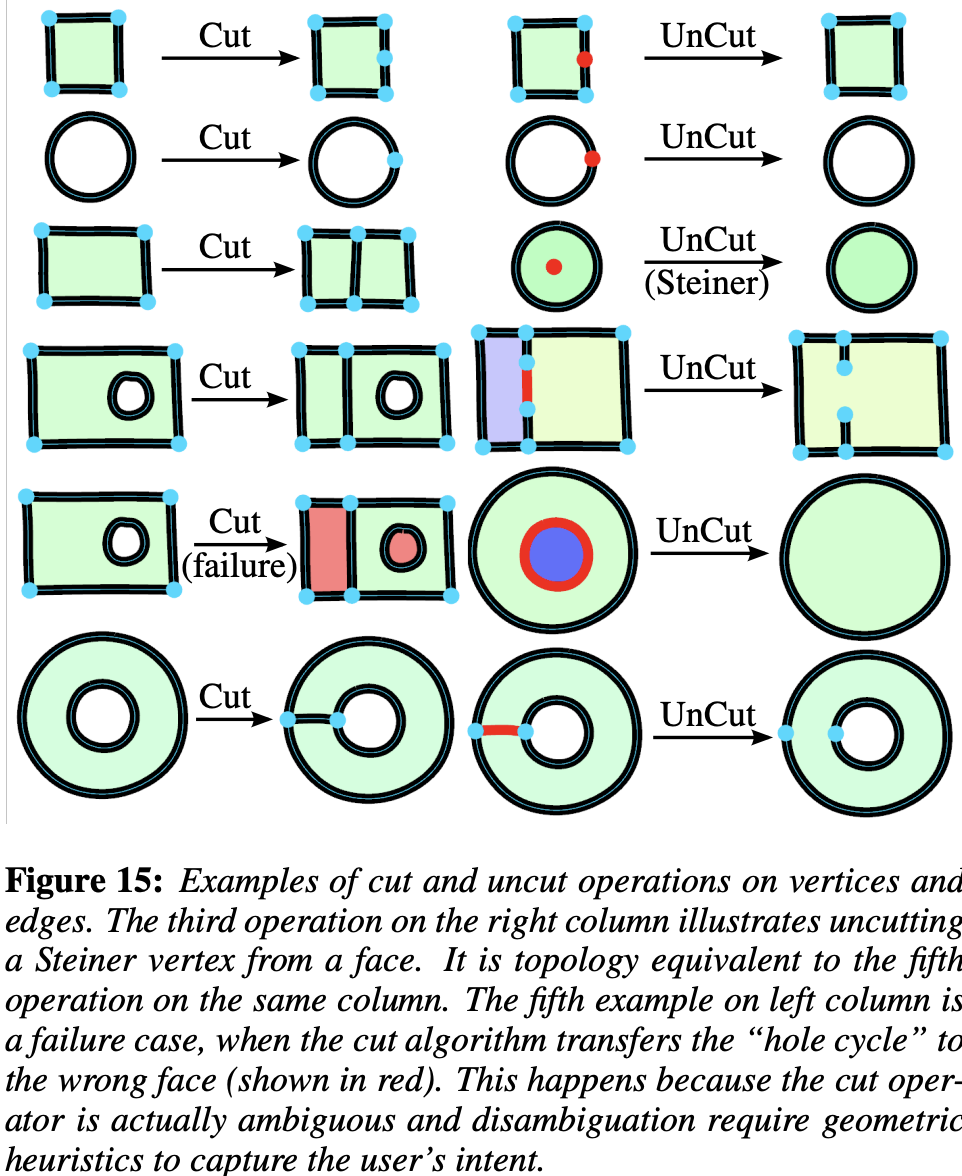
Cut & uncut